题目内容
【题目】25.（20分）如图，两水平面（虚线）之间的距离为H，其间的区域存在方向水平向右的匀强电场。自该区域上方的A点将质量为m、电荷量分别为q和–q（q>0）的带电小球M、N先后以相同的初速度沿平行于电场的方向射出。小球在重力作用下进入电场区域，并从该区域的下边界离开。已知N离开电场时的速度方向竖直向下；M在电场中做直线运动，刚离开电场时的动能为N刚离开电场时的动能的1.5倍。不计空气阻力，重力加速度大小为g。求
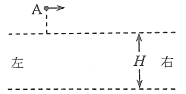
（1）M与N在电场中沿水平方向的位移之比；
（2）A点距电场上边界的高度；
（3）该电场的电场强度大小。
【答案】（1）3:1（2）
（3）
【解析】
（1）设带电小球M、N抛出初速度均为v0，则它们进入电场时的水平速度仍为v0；MN在电场中的运动时间t相等，电场力作用下产生的加速度沿水平方向，大小均为a，在电场中沿水平方向的位移分别为s1和s2；由运动公式可得：
v0-at=0 ①
②
③
联立①②③解得：
④
（2）设A点距离电场上边界的高度为h，小球下落h时在竖直方向的分速度为vy，则；
⑤
⑥
因为M在电场中做匀加速直线运动，则
⑦
由①②⑤⑥⑦可得h=⑧
（3）设电场强度为E，小球M进入电场后做直线运动，则
⑨
设MN离开电场时的动能分别为Ek1、Ek2，由动能定理：
⑩
由已知条件：Ek1=1.5Ek2
联立④⑤⑥⑦⑧⑨⑩解得: 
练习册系列答案
名校课堂系列答案
相关题目
