题目内容
【题目】如图,直线DE与⊙O相切于A,AB是⊙O的弦,∠EAB的平分线交⊙O于点C,连接CB,并延长直线EA相交于点D.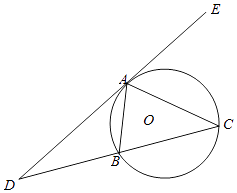
(1)求证:DAAC=DC2﹣DA2;
(2)若AD=6,AC=5,求弦AB的长.
【答案】
(1)证明:∵直线DE与⊙O相切于A,AB是⊙O的弦,∠EAB的平分线交⊙O于点C,
连接CB,并延长直线EA相交于点D,
∴∠BAC=∠EAC=∠ABC,∴AC=AB,
∴DC2﹣DA2=DC2﹣DBDC=DC(DC﹣DB)=DCBC=DCAC.
∴DAAC=DC2﹣DA2.
(2)解:设DB=x,由DA2=DBDC,得x(x+5)=36,
解得x=4,
∵直线DE与⊙O相切于A,∴∠DAB=∠ACD,
∵∠ADB=∠ADC,∴△DAB∽△DCA,
∴ ![]() ,
,
∵AD=6,AC=5,∴ ![]() ,解得
,解得 ![]() .
.
【解析】1、由余弦定理以及∠EAB的平分线交⊙O于点C,得到∠BAC=∠EAC=∠ABC,即得AC=AB。利用割线定理证明结论。
2、根据割线定理可求出DB=4,进而推导出△DAB∽△DCA,即求出AB的长。

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目