Question

【题目】如图所示，正方形均质板重，用4根轻质杆铰链水平悬挂，外形构成边长为的立方体，现将方板绕铅垂对称轴旋转角度，再用一细绳围绕四杆的中点捆住，使板平衡于角位置。试求绳内的张力.

Answer 1

【答案】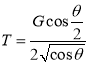

【解析】

把木板绕铅垂对称轴旋转角度以后，系统虽然不是一个很对称的立方体，但把系统绕通过中心的铅直轴旋转90°的整数倍，系统的位形将与转动之初的位形重合，说明四根轻杆的受力情况是完全一样的，系统是对称的. 系统处于平衡状态时，把四根轻杆、木板、绳组成的部分看成刚体，刚刚体受四个铰接部分的力二平衡，由重力方向的平衡可以得出，竖直方向对每根轻杆的拉力为

. ①

而铰接处是否对轻杆有水平方向的作用力，暂时还不好确定，不过可以设为，从俯视图来看四根轻杆的受力情况（如图乙所示）.

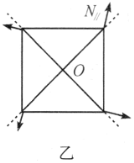
图中虚线表示正方形对角线的外延部分，如果不在对角线方向上，则四个对点有一个力偶矩，将使得下面的部分旋转，与平衡假设相矛盾，因此水平弹力必然在对角线方向，要么都向外，要么都向里（设向外为正，这种设法不会影响结果）.

同样的道理，把木板隔离开来，可知木板对轻杆往下的拉力为

. ②

而水平方向的作用力必沿对角线方向（否则木板旋转），木板对杆的作用力向里、向外的性质与上端铰链的方向相同，否则以绳对杆的作用点为支点，力矩无法平衡.

下面再看整个系统的俯视图（如图丙所示），把轻杆隔离出来作为平衡的刚性杆，利用力的平衡条件和力矩的平衡条件可求出拉力的大小.

绳作用在每根转杆的中点，在俯视图上不难看出，绳子构成一个正方形，且在水平面内，因而可以知道绳对轻杆仅有水平面内的拉力，轻杆在竖直方向上力的平衡是满足的，则

. ③

取一根轻杆为研究对象，不难求出与的关系，以及与的关系. 设绳的张力为，则水平合力.

方向水平力平衡，有

； ④

方向水平力平衡，有

. ⑤

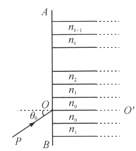
在过轻杆的竖直面内来分析力矩平衡（只研究平面内转矩），如图丁所示.

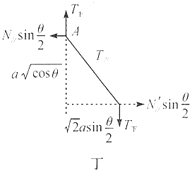
对于点，力矩平衡，有

. ⑥

联合②④⑤⑥式可得.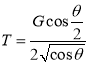

初看此题，一般都会觉得比较复杂，因为题中铰链就看8个，加上4根轻质杆与绳子有4个接触点，一共有12个受力点，而且，初看甚至想象不出木板旋转角度以后整个系统是什么样子，即使把各个受力点的力逐个画出来也无济于事.

对于这种复杂的系统，如同本题一样，对称分析（等价）往往是解决问题的突破口，找出最基本的部分，再把空间方向确定下来，然后画出各个力点的受力情况，再依据规律求解.

另外，对于复杂的静平衡问题，运用虚功原理也是一种有效的手段. 本题亦可通过虚功原理求解，但这同样面临着空间几何问题方面的障碍.