Question

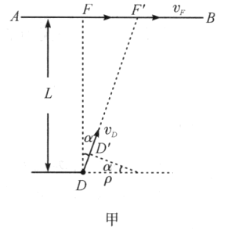
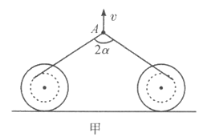
【题目】两个线圈位于水平面上，其中间部分缠有不可伸长的轻线（如图甲所示）。这条线上的A点与两线圈轴等距离，A点开始竖直向上移动。这时线圈开始做无滑动的滚动，其轴不改变自己的方向，线也不沿线圈滑动，不在线圈上的线段位于垂直线轴的竖直平面内。问：当A点速度等于v，时，两线圈靠近的速率u多大？（线圈中间部分半径与线圈侧板半径的比）

Answer 1

【答案】

【解析】

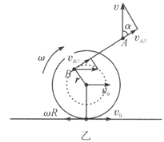
由于线不可伸长，线上所有点沿线方向分速度相等。因此，当A点以速度v竖直向上运动时，该点左边线段与竖直线成角，如图乙所示，线段AB上各点沿线方向分速度相等，即。

如果用表示左线圈轴运动速度，用表示该线圈相对其轴转动的角速度，考虑到线圈没有相对水平面滑动，那么可以列出，式中，为线圈侧板半径。

据题意，线不沿线圈滑动，所以线圈上B点以及线上B点沿线方向分速度相等，即。因此，左线圈轴运动速度为。

从对称性考虑，左、右线圈轴相对水平面速度大小相等但方向相反，于是所求两线圈靠近的速率为。