题目内容
【题目】已知函数 ![]() .
.
(i)当 ![]() 时,满足不等式
时,满足不等式 ![]() 的
的 ![]() 的取值范围为 .
的取值范围为 .
(ii)若函数 ![]() 的图象与
的图象与 ![]() 轴没有交点,则实数
轴没有交点,则实数 ![]() 的取值范围为 .
的取值范围为 .
【答案】![]() ;
;![]()
【解析】(i)当 ![]() 时,不等式为
时,不等式为 ![]() 。等价于
。等价于 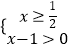 或
或 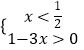 ,
,
解得 ![]() 或
或 ![]() ,
,
∴ ![]() 的取值范围为
的取值范围为 ![]() 。
。
(ii)∵函数 ![]() 的图象与
的图象与 ![]() 轴没有交点,
轴没有交点,
∴函数 ![]() 与函数
与函数 ![]() 的图象没有公共点。
的图象没有公共点。
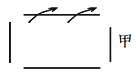
①当 ![]() 时,画出
时,画出 ![]() 与函数
与函数 ![]() 的图象如图:
的图象如图:
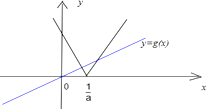
可得两函数的图象恒有交点,不合题意。
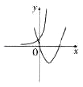
②当 ![]() 时,画出
时,画出 ![]() 与函数
与函数 ![]() 的图象如图:
的图象如图:
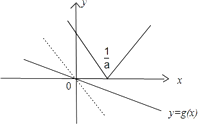
结合图象可得,要使两个图象无交点,则斜率满足: ![]() ,
,
解得 ![]() ,故
,故 ![]() 。
。
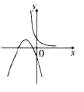
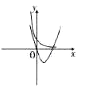
③当 ![]() 时,画出
时,画出 ![]() 与函数
与函数 ![]() 的图象如图:
的图象如图:

可得两函数的图象恒有交点,不和题意。综上得 ![]() 。
。
答案:(i) ![]() (ii)
(ii) ![]()
【考点精析】解答此题的关键在于理解绝对值不等式的解法的相关知识,掌握含绝对值不等式的解法:定义法、平方法、同解变形法,其同解定理有;规律:关键是去掉绝对值的符号.

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目