Question

【题目】如图所示，光滑水平桌面上静止放置着若干个相同的匀质小球，打击其中某个球，让其与别的球发生碰撞，球与球间的碰撞都是弹性碰撞，若第一个被撞球经一闭合线路后又可停在原位置上，问：桌面上至少需要放多少个球？

Answer 1

【答案】5个

【解析】

先证明一个引理：一弹性球与另一静止的相同的小球发生碰撞，碰撞后两小球将以相互垂直的方向运动。

证明如下：在质心系中，两小球的总动量为零，则两小球碰撞后速度大小不变，且等大反向。

所以，在桌面系中，两球的速度将垂直。

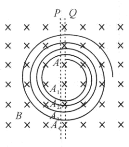
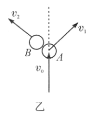
也可以用图乙所示的碰撞情况加以说明：A球以与B球发生碰撞，在A、B两球的球心连线方向上将发生速度交换，所以，碰后B球将在该方向上以速度运动，A球的速度在该方向上为零，而A球在两球球心连线的垂直方向上不受力的作用，碰后将保持速度在该方向上运动，显然。

在本题中，小球每与静止的小球碰撞后，其偏向角，而任何闭合图形的外角和为360°，在小球发生碰撞处，小球每次的偏向角（多边形的外角）都小于90°，但回到原点处不受这一约束，则这一多边形至少有4个顶点。要使最初撞击的球最终停在原位置，则多达形的4个顶点都必须放一个球，如果再加上撞击球，桌面上一共应该有5个小球。