题目内容
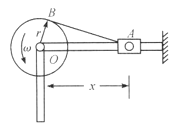
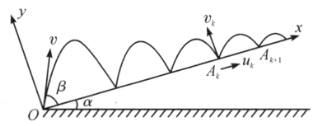
【题目】如图所示,倾角为![]() 的一个光滑斜面,由斜面上一点O通过斜面最大斜率的竖直平面内斜上抛一个小球,初速度为v,抛出方向与斜面交
的一个光滑斜面,由斜面上一点O通过斜面最大斜率的竖直平面内斜上抛一个小球,初速度为v,抛出方向与斜面交![]() 角,
角,![]() 。
。
(1).若小球与斜面的每次碰撞不消耗机械能,并且小球在第n次与斜面相碰时正好回到抛射点O,试求![]() 、
、![]() 、n满足的关系式。
、n满足的关系式。
(2).若小球与斜面每次碰撞后,与斜面垂直的速度分量满足:碰后值是碰前值的e倍,![]() 。并且小球在第n次与斜面相碰时正好回到抛射点O,试求
。并且小球在第n次与斜面相碰时正好回到抛射点O,试求![]() 、
、![]() 、n和e满足的关系式。
、n和e满足的关系式。
(3).由2,若其中第r次与斜面相碰时,小球正好与斜面垂直相碰,试证明此时满足关系式:![]() 。
。
【答案】1.![]()
![]() 2.
2.![]() 3.见解析
3.见解析
【解析】
(1)建立如图所示的直角坐标系.斜上抛的小球在y轴方向上有多次的往复运动,而在x轴方向上只有一次。设![]() 为小球第k次与斜面相碰的点,
为小球第k次与斜面相碰的点,![]() 、
、![]() 是小球第k次与斜面相碰后速度在x、y方向上的分量,加速度为
是小球第k次与斜面相碰后速度在x、y方向上的分量,加速度为
![]() ,
,![]() 。
。
![]() 到
到![]() 的时间
的时间![]() 满足
满足
![]() ,即
,即![]() 。
。
由此可以得到小球从O点抛出开始,直至抵达![]() 所经历的时间为
所经历的时间为
![]()
![]() 。
。
因为小球与斜面的每次碰撞中并不消耗能量,所以,
![]()
所以,![]() 。
。
因斜面是光滑的,再利用x轴方向的分量运动方程,当小球与斜面碰撞n次时有![]() ,
,
即![]() 。
。
联立![]() 与
与![]() (用n替代
(用n替代![]() 中的k)可以得到
中的k)可以得到![]() 。
。
(2)利用(1)中小球从O点抛出开始,直至抵达![]() 所经历的时间
所经历的时间![]() ,
,
小球与斜面垂直的分量满足![]()
所以,![]()
![]() 。
。
再利用![]() ,联立上式,整理可以得到
,联立上式,整理可以得到
![]() 。
。
(3)接上问,现小球在第r次与斜面相碰时与斜面垂直,即![]() ,而
,而
![]() ,
,
即![]() 。
。
利用![]() (其中k用r代之),联立
(其中k用r代之),联立![]() ,整理后得
,整理后得![]() ,
,
将![]() 代入,即可得
代入,即可得![]() .
.
本题的命题方式是在同一模型背景下,设计出不同层次的问题,且随着问题的升级,涉及的信息量、干扰问题的因子、计算量等也随之增加,对不同层面的答题者作出了有效的区分,本题中问题是通过小球与斜面的碰撞从弹性到非弹性,再到碰撞时小球沿斜面方向与垂直于斜面方向的约束关系的确定,将问题一步一步地向上推。
事实上,设置了多问的试题大多都有这一功能,对这类试题的解答我们应该量力而行,努力完成自己能够完成的部分内容。