题目内容
【题目】质量分别为![]() ,
,![]() 的两物体
的两物体![]() 、
、![]() 连接在原长
连接在原长![]() ,劲度系数为
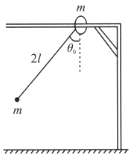
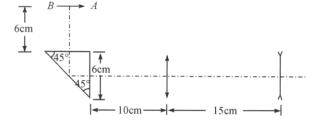
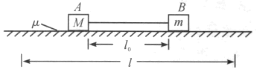
,劲度系数为![]() 的弹性绳两端,并放置在水平桌面上,如图所示.已知两物块与桌面间的摩擦因数均为
的弹性绳两端,并放置在水平桌面上,如图所示.已知两物块与桌面间的摩擦因数均为![]() .现将两物拉开至相距
.现将两物拉开至相距![]() 处,由静止释放,试求:
处,由静止释放,试求:
(1)两物体相碰时的速度![]() 、
、![]() ;
;
(2)从释放到相碰所用的时间.
【答案】(1)![]()
![]()
(2)![]()
【解析】
(1)系统的运动可分解为质心的运动和相对于质心的运动.由于存在外力,故先求质心运动的加速度.
由牛顿第二定律可得
![]() ,
,
所以,![]() .
.
下面讨论两物体相对于质心的运动.
当![]() 、
、![]() 之间的距离为
之间的距离为![]() 时,
时,![]() 、
、![]() 到质心的距离分别为
到质心的距离分别为![]() 和
和![]() ,则对应部分弹性绳的劲度系数分别为
,则对应部分弹性绳的劲度系数分别为![]() 和
和![]() .
.
由于质心系是一个零动量的系统,我们选择其中一个物体作为研究对象,得到绳子松弛时的速度,也就容易得到另一个物体的速度.
讨论质心系中![]() 的运动.
的运动.
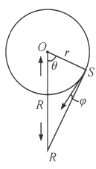
如图所示,![]() 为绳子的松弛点,则
为绳子的松弛点,则
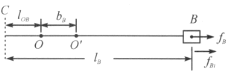
![]() .
.
![]() 为
为![]() 在弹力、摩擦力
在弹力、摩擦力![]() 和惯性力
和惯性力![]() 共同作用下的平衡点,所以
共同作用下的平衡点,所以
![]() ,
,
所以,![]() .
.
而拉伸后,![]() ,所以,
,所以,![]() 在弹性绳收缩的过程中做振幅为
在弹性绳收缩的过程中做振幅为![]() 的简谐运动,其周期
的简谐运动,其周期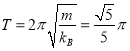 .
.
![]() 从释放到回到原长所经历的时间
从释放到回到原长所经历的时间![]() 满足
满足
![]() .
.
代入数据可得
![]() .
.
![]() 到达
到达![]() 点时的速度为
点时的速度为![]() ,则
,则
![]() .
.
代入数据可得![]() .
.
利用质心系的动量是零可得
![]() .
.
回到桌面参考系中,质心的速度为
![]() .
.
![]() 的速度为
的速度为
![]() .
.
![]() 的速度为
的速度为
![]() .
.
以后绳子在松弛状态,两物体运动的加速度大小均为
![]() .
.
由于![]() 的速率较小,先计算此刻起到停止为止,经历的时间
的速率较小,先计算此刻起到停止为止,经历的时间![]() ,滑过的路程
,滑过的路程![]() .
.
![]() ,
,
![]() .
.
在![]() 时间内,
时间内,![]() 的运动路程为
的运动路程为
![]() ,
,
![]() .
.
说明在![]() 停下来以前,
停下来以前,![]() 、
、![]() 未发生碰撞.重新考察
未发生碰撞.重新考察![]() 的运动,有
的运动,有
![]() .
.
假设![]() 经过
经过![]() 后还有速度
后还有速度![]() ,有
,有
![]() ,
,
解得![]() .
.
两物体相碰时的速度为
![]() ,
,![]() (“—”表示方向向左).
(“—”表示方向向左).
(2)前面已经得到了![]() ,下面再求从绳子松弛开始到
,下面再求从绳子松弛开始到![]() 、
、![]() 相碰所经历的时间
相碰所经历的时间![]() .
.
利用![]() 得
得![]() ,
,
所以,![]() .
.
本题是一道较为复杂的动力学习题,对象与过程都较多,而且每个对象的过程都不是单一的,其运动也不是同步的,因此,在对每个对象运用程序法解题时,还必须注意与另一对象的对比,其难度可想而知.
参照系的选择是捅破本题的一大亮点,此处质心系一方面是零动量系,同时也是非惯性系,零动量系为求解物体的速度带来了方便,但非惯性系中的动力学问题又必须引入惯性力,而且最后还必须回到地面系来研究问题,得到结果,可谓有得矣有失,但从总体上讲,质心系为我们的解题带来的描述上的简洁是其他方法无法替代的.
单个物体在有摩擦力作用的情况下的振动,我们平时研究得较多,这种运动单向是简谐运动,但双向并不是完整的简谐运动,因为不同方向振动的平衡位置并不相同,因此,这类习题的解题必须严格地遵循程序法的解题步骤.