题目内容
【题目】若关于x的不等式|ax﹣2|＜3的解集为{x|﹣ 
＜x＜ 
}，则a= ．
【答案】-3
【解析】解：显然，a=0时，条件|ax﹣2|＜3恒成立，不满足解集为{x|﹣ 
＜x＜ 
}．
当a＞0时，由关于x的不等式|ax﹣2|＜3可得﹣3＜ax﹣2＜3，解得﹣ 
＜x＜ 
，
再根据的解集为{x|﹣ ＜x＜ }，∴ 
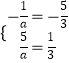，a无解．
当a＜0时，由关于x的不等式|ax﹣2|＜3可得﹣3＜ax﹣2＜3，解得 ＜x＜﹣ ，
再根据的解集为{x|﹣ ＜x＜ }，∴ 
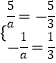，解得a=﹣3，
故答案为：﹣3．
分a=0、a＞0、a＜0三种情况，分别去掉绝对值求得不等式的解集，再把求得的解集和所给的解集作对比，从而求得a的值，综合可得结论．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
