Question

【题目】如图甲所示，半长轴和半短轴分别为a和b的一个椭圆，假定长轴是竖直方向。有一质量为m的质点沿椭圆的“直径”下滑，问：此质点沿此椭圆的哪一“直径”下滑至原点所需的时间最短？

Answer 1

【答案】当时，质点沿过的“直径”滑下时，到达原点所用的时间最短。当时，质点沿竖直的“直径”滑下时，到达原点所用的时间最短。

【解析】

如图乙所示，从球O的最高点A向球面上引一条轨道AC，图中AB为球面在竖直方向上的直径，设球的半径为R，由几何知识知。

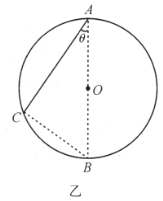
当一质点在重力作用下沿AC滑下时，由牛顿第三定律可知，其加速度为。

则质点由A滑到C所用的时间t满足，即，所以。

此式表明，质点下滑的时间与无关，亦即与C点的位置无关。

即在球面的最高点与球面上任意一点之间建立一条光滑的直线轨道，让一质点在重力作用下从球面的顶点沿轨道滑到球面上，则该质点在任意轨道上运动的时间是相等的。

由运动的对称性，在竖直圆环上向圆环的最低点引直线轨道，质点在重力作用下沿所有的直线轨道运动的时间是相等的。

据此，要确定椭圆的“直径”，便要找到最低点在原点O且与椭圆内切的圆。设此圆的半径为R，则圆的方程为。

又该椭圆的方程为，

联立上述两方程可得。

若椭圆与圆相切，则y只有一解，所以

。

此时。

由此可得。

此外，R必须满足，即，解得。

所以，当时，质点沿过的“直径”滑下时，到达原点所用的时间最短。

当时，质点沿竖直的“直径”滑下时，到达原点所用的时间最短。