题目内容
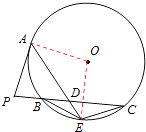
【题目】如图,P是⊙O外一点,PA是切线,A为切点,割线PBC与⊙O相交于点B,C,PC=2PA,D为PC的中点,AD的延长线交⊙O于点E,证明: 
(1)BE=EC;
(2)ADDE=2PB2 .
【答案】
(1)证明:连接OE,OA,则∠OAE=∠OEA,∠OAP=90°,
∵PC=2PA,D为PC的中点,
∴PA=PD,
∴∠PAD=∠PDA,
∵∠PDA=∠CDE,
∴∠OEA+∠CDE=∠OAE+∠PAD=90°,
∴OE⊥BC,
∴E是 ![]() 的中点,
的中点,
∴BE=EC;
(2)证明:∵PA是切线,A为切点,割线PBC与⊙O相交于点B,C,
∴PA2=PBPC,
∵PC=2PA,
∴PA=2PB,
∴PD=2PB,
∴PB=BD,
∴BDDC=PB2PB,
∵ADDE=BDDC,
∴ADDE=2PB2.
【解析】(1)连接OE,OA,证明OE⊥BC,可得E是 ![]() 的中点,从而BE=EC;(2)利用切割线定理证明PD=2PB,PB=BD,结合相交弦定理可得ADDE=2PB2 .
的中点,从而BE=EC;(2)利用切割线定理证明PD=2PB,PB=BD,结合相交弦定理可得ADDE=2PB2 .

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目