题目内容
【题目】如图所示,质量均为m的两个质点A和B,由长为l的不可伸长的轻绳连接,B质点被限制在水平面上的光滑直槽内,A、B垂直于直槽且相距为![]() 。若质点A以速度v在桌面上平行于槽的方向运动,求质点B开始运动时的速度大小。
。若质点A以速度v在桌面上平行于槽的方向运动,求质点B开始运动时的速度大小。

【答案】![]()
【解析】
方法1 质点系在原来速度v的方向上动量守恒,但绳在张紧时刻时v沿绳方向的速度已有损失。根据动量守恒定律及动量定理即可求解。
绳张紧时刻球A在垂直于绳方向上的速度不发生变化,![]() ,沿绳方向的速度已经变化,设为
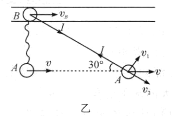
,沿绳方向的速度已经变化,设为![]() 。若张紧时刻绳子张力的冲量大小为I,各量的方向如图乙所示,则对A和B分别有
。若张紧时刻绳子张力的冲量大小为I,各量的方向如图乙所示,则对A和B分别有
![]() ,
,
![]() 。
。
因为A、B由绳子牵连,所以它们沿绳方向的速度分量应相等。
![]() 。
。
联立求解以上三式可得![]() 。
。
方法2 对系统运用动量守恒定律,即
![]() 。
。
![]() ,
,
得![]() 。
。

练习册系列答案
相关题目