题目内容
【题目】有一种假设，星球由星球之间的介质（宇宙尘埃）在引力作用下经压缩方式而形成.估算由宇宙尘埃的巨大球团组成星球的时间.可以认为压缩时微粒互不超越.宇宙尘埃的密度
，万有引力恒量
.
【答案】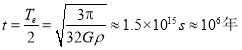
【解析】
研究离球团中心
处球团尘埃的微粒.它只受到位于半径为的球内微粒的引力作用.据题意，微粒互不超越，吸引该微粒的总质量保持不变.设想其全部质量集中在团中心，于是问题归结为寻找微粒落到引力中心的时间.
我们将微粒向中心的运动看作是沿十分扁长椭圆运动的极限情况，椭圆长半轴为
，并将该运动与半径为的圆轨道转动相比较.应用开普勒第三定律：
，
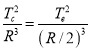式中
为沿圆周轨道运动周期，
为沿椭圆轨道运动周期.根据牛顿第二定律以及万有引力定律不难求出周期：
，
，
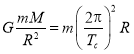由此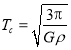
，
.
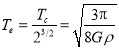我们得到，周期与无关.因此，微粒落到引力中心的时间（星球形成时间），为沿椭圆轨道转动周期的一半，与宇宙尘埃团的半径无关，且
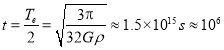年.
本题的第一个要点是应注意到每个微粒在互不超越的前提下，它只受到位于半径为的球内微粒的引力作用，这是平方反比的有心力；第二则是粒子的运动虽是直线，但仍应视为椭圆，且引力中心不是这一线段的中点，而是一个端点.很多同学会依据对称认为引力中心是轨道的中点，这是违背开普勒定律的.
天体在有心引力作用下的运动，依据开普勒定律，其轨迹应为椭圆，但我们应该注意到，圆（半长轴与半短轴相等，都等于圆的半径，焦点为圆心）与直线段（半短轴为零，线段长为长轴，焦点在线段的端点）是椭圆的两个极端的特例，当天体做与此相关的运动时，同样也是遵循开普勒定律的.以直线段为背景的天体运动在竞赛中较为常见，应注意练习.
练习册系列答案
相关题目
