Question

【题目】如图所本，一个半径为R的透明材料制成的球，AB为其一条直径，两点附近的球表面透光，球表面的其他大部分地方均涂黑而不透光。今在球内B处有一个小发光泡。

(1).在球的左侧外部AB直线上进行观察时，试讨论像的位置与球的折射率的关系。

(2).若球的折射率为n，像在球的右侧，则小泡的像距B点多远？

(3).(2)问中像的垂轴放大率为多少？

(4)．若在球的左侧贴近A处置一平面镜，其镜面与AB垂直，与球面相切，试问n为何值时，可使2中所成的虚像，再经过此系统的作用最后在球的右侧形成实像。

Answer 1

【答案】（1）当时，，不成像（或成像于无限远处）；时，，成实像（在Α点左侧）；时，，成虚像（在Α点右侧），又，故，即当时，像必在B点右侧，如图中的。

（2）（3）（4）

【解析】

(1)光线自右至左，为单折射球面近轴成像问题。如图乙所示，设球的折射率为n，其物距为，设像距为，则由成像公式，有

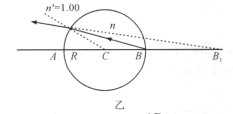
，即，

由此可见，当时，，不成像（或成像于无限远处）；时，，成实像（在Α点左侧）；时，，成虚像（在Α点右侧），又，故，即当时，像必在B点右侧，如图中的。

(2)在时，虚像点离物点Β的距离为

。

(3).(2)问中像的垂轴放大率

。

（4）.若如图丙所示，在Α处置一平面镜，则共有四次成像过程：

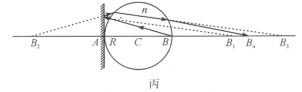
第一次，经左半球面的折射成虚像于，其物距，由前面的结果知，此时的像距。虚像位于B点右侧的条件为。

第二次，，经平面镜反射成像（），其物距，则像距。

第三次，再经左半球面折回成像（），这时物距，由成像公式有，

由此求出。

第四次，经右半球面成像（），物距为

。

于是由得到

。

按题意，最后的像在球的右侧（实像），这要求，即

。

由前面已知，，故上式左端分子大于零，因此有

，

其解为

已知，故得符合本题条件的n值为。