题目内容
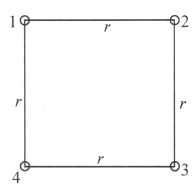
【题目】如图所示,4个半径为![]() 的相同导体球位于边长为r的正方形的4个顶点上,球1带电Q,用金属丝依次连接球1和球2,球1和球3,球1和球4,最后连接球1和地.设每次接通都能达到静电平衡,不计金属丝上可能带的电荷,求流入大地的电量。
的相同导体球位于边长为r的正方形的4个顶点上,球1带电Q,用金属丝依次连接球1和球2,球1和球3,球1和球4,最后连接球1和地.设每次接通都能达到静电平衡,不计金属丝上可能带的电荷,求流入大地的电量。
【答案】
【解析】
每次都能达到静电平衡,就是每次接触金属丝两端都能达到等势。但每一端的电势都要计及各个电荷的贡献,都要进行叠加.
球1接触球2且平衡后,球1带![]() ,
,![]() .球1接触球3且平衡后,由于分布具有对称性,即球1与球3以球2和球4的对角线对称,球2与球1的电荷在球1上产生的电势跟球2与球3的电荷在球3上产生的电势相等(注意,如果球1先接触球2后接触球4,就没有对称性了),所以,球1带电量变为
.球1接触球3且平衡后,由于分布具有对称性,即球1与球3以球2和球4的对角线对称,球2与球1的电荷在球1上产生的电势跟球2与球3的电荷在球3上产生的电势相等(注意,如果球1先接触球2后接触球4,就没有对称性了),所以,球1带电量变为![]() ,
,![]() .
.
球1接触球4,平衡后4个电荷的分布已不具备对称性,但必有![]() ,.这时4个电荷(除
,.这时4个电荷(除![]() 与
与![]() 外,另设
外,另设![]() 与
与![]() )在球1上和球4上都贡献电势,
)在球1上和球4上都贡献电势,![]() 与
与![]() 分别是4个电势叠加的结果,另据电荷守恒律,有
分别是4个电势叠加的结果,另据电荷守恒律,有
![]() ,
,
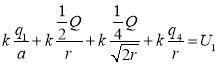 ,
,
 .
.
联立两个方程式,可以解出![]() 与
与![]() ,其中利用到
,其中利用到![]() 即
即![]() 的条件。
的条件。
 ,
,
球1接触地,平衡后![]() .设这时球1带电量为
.设这时球1带电量为![]() ,据叠加原理,有
,据叠加原理,有
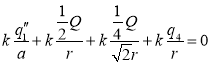
解得
负号表示球1这时带负电.
因为![]() 为正电,说明球1接触地时,流入大地的电荷
为正电,说明球1接触地时,流入大地的电荷![]() .
.


 .
.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目