题目内容
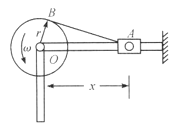
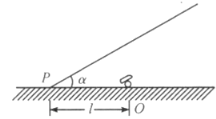
【题目】火炮从掩蔽所下向外发射炮弹,掩蔽所与水平成![]() 角,炮位O与掩蔽所顶点P相距l,如图所示,炮弹发射的初速度为
角,炮位O与掩蔽所顶点P相距l,如图所示,炮弹发射的初速度为![]() w,试求炮弹的最远射程。
w,试求炮弹的最远射程。
【答案】见解析.
【解析】
以O点为坐标系原点,取平行于掩蔽所方向为x轴方向,垂直于掩蔽所的方向为y轴方向,如图乙所示.
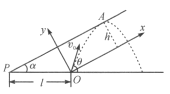
在此坐标系中,炮弹运动在y方向的初速度和加速度分别为
![]() 。
。
若炮弹运动轨道与掩蔽所相切,则相切点A的y坐标值为
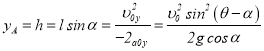 ,
,
即![]() 。
。
由上式,可作以下讨论:
(1)若![]() ,则炮弹的轨道不可能与掩蔽所相切,故只要取
,则炮弹的轨道不可能与掩蔽所相切,故只要取![]() ,炮弹就可获最大射程,为
,炮弹就可获最大射程,为
![]() 。
。
(2)若![]() ,由
,由![]() 可知,炮弹发射角取以下值时,其轨道与掩蔽所相切:
可知,炮弹发射角取以下值时,其轨道与掩蔽所相切:![]() ,所以
,所以
(i)若上式表示的![]() ,即
,即![]() ,
,
则只要取![]() ,炮弹就可获最大射程
,炮弹就可获最大射程![]() 。
。
(ii)若![]() ,即
,即![]() ,则炮弹的发射角
,则炮弹的发射角![]() 取
取![]() ,炮弹就可获最大射
,炮弹就可获最大射
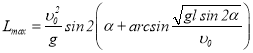 。
。
对于抛体运动问题,物体(质点)运动障碍的处置与临界状态的分析是我们解答的两大障碍。
就目前已有的题型来看,其障碍物的设置除了直立物体、天花板、斜面、二交函数构成的区域之外,命题人有一种将问题向形状更为复杂的障碍体上推进的可能,而这种更为复杂的推进,带来的必定是更为隐蔽的临界状态和更大的运算量,要求答题者具备更强的综合运用知识的能力,大家应做好这方面的准备。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目