题目内容
【题目】在![]() 平面内分布着某种透明光学材料,已知折射率分布
平面内分布着某种透明光学材料,已知折射率分布![]() ,
,![]() 为点到原点的距离,在距原点
为点到原点的距离,在距原点![]() 处的A点有一点光源,若从此点光源发出的光在该材料中,沿以
处的A点有一点光源,若从此点光源发出的光在该材料中,沿以![]() 为焦点的圆锥曲线传播,求折射率的分布规律
为焦点的圆锥曲线传播,求折射率的分布规律![]() ,已知
,已知![]() .
.
【答案】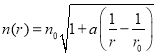 其中
其中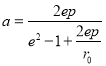
【解析】
以![]() 为原点,
为原点,![]() 轴为极轴建立极坐标.将平面以极点为中心,分成一个个同心薄圆环,宽度
轴为极轴建立极坐标.将平面以极点为中心,分成一个个同心薄圆环,宽度![]() ,如图所示,则每个圆环区城内的折射率相同,由折射定律有
,如图所示,则每个圆环区城内的折射率相同,由折射定律有
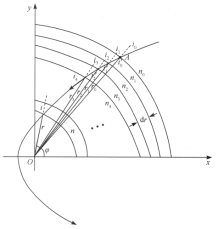
![]() ,
,
![]() ,
,
![]() ,
,
根据正弦定理,又有![]() .
.
由以上各式可以得出![]()
![]() ,
,
即![]() 常数,与角动量守恒定律表达式:
常数,与角动量守恒定律表达式:![]() 常矢量,有相似之处,可将
常矢量,有相似之处,可将![]() 类比于动量
类比于动量![]() ,则
,则![]() 类比于动能
类比于动能![]() .
.
在平方反比引力下,质点运动的动能为![]() .
.
![]() 为总能量,为常数,且
为总能量,为常数,且![]() .
.
势能函数为![]() (
(![]() 为常数),所以,
为常数),所以,![]() .
.
由类比,得到![]() (
(![]() 为常数)所以,
为常数)所以, .
.
令![]() ,而
,而![]() ,
,
此时![]() ,A为半长轴,即
,A为半长轴,即![]() ,
,
其中轨迹方程为![]() ,则
,则![]() .
.
代入解得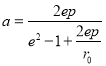 ,即
,即 ,其中
,其中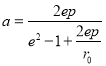 .
.
本题同样是光在非均匀介质中的传播,其轨迹给定为圆锥曲线,其解答是类比法的经典之作,读者应认真研究.类比思维在处理物理问题中有很高的地位,它要求问题的处理者能清醒地认识到不同领域的问题间存在相同或类似的物理或数学规律,可以将我们所熟悉的方法或结论迁移到需要研究的领域中.这类思维方法在竞赛中有着广泛的应用,读者可以作相应的归类分析、应用。

练习册系列答案
 华东师大版一课一练系列答案
华东师大版一课一练系列答案 孟建平名校考卷系列答案
孟建平名校考卷系列答案
相关题目