Question

【题目】半径为的刚性球固定在水平桌面上，有一个质量为的圆环状均匀弹性细绳圈，原长，，细绳圈的劲度系数为（绳伸长时，绳中弹性张力为）.将绳圈从球的正上方轻放到球上，并用手扶着绳圈使其保持水平并最后停留在某个平衡位置，如图所示。

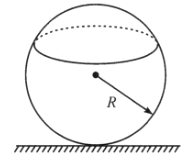
（1）设平衡时绳圈长为，，忽略摩擦，考虑重力，试求劲度系数（用表示）.

（2）设，求绳圈的最后平衡位置及长度.

Answer 1

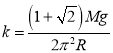【答案】（1） ；（2）

【解析】

设平衡时绳圈位于球面上相应于角的纬线上,考虑绳上的一段长为的一小段,俯视图如图所示,这一小段的重力为,方向竖直向下.绳内的张力大小为,所以,张力的合力大小为,方向在平面内并指向绳圈的中心球面对这一小段的支持力,方向沿球的半径向外,这三个力在同一个竖直平面内,将这三个力在该平面内沿球面的径向与法向进行分解,可确定绳在球面上的平衡状态。

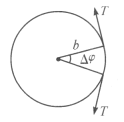
(1)由球面经线切向合力为零有

, （*）

式中，

解得。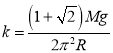

(2)当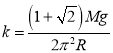时,由(*)式及相关数据可得：

,即 .

注意到,且，所以上式无解.实际上,太小时,绳圈在重力作用下将滑过球体而落在桌面上,因此绳长为原长，即。

解答本题,至少有下面三点需要我们突破:

1.本题显然是一个力的平衡问题,选绳子整体为对象显然不合适,而从中隔离出微元部分作为研究对象,需要我们有隔离法的思想。

2.当以隔离出的一小段为研究对象时,其所受力不在一个平面内,是空间力系,要能对其进行降维处理,将空间力系转换为几个平面力系,进而在平面力系中进行相关的研究。

3.当在(2)中得到无解后,要意识到绳子在球面上是不存在平衡态的,必然是绳子落地,收缩至原长,且最终还必须给出结果。