题目内容
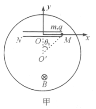
【题目】如图所示,在半径为![]() 的无限长圆柱形区域内有匀强磁场,磁场
的无限长圆柱形区域内有匀强磁场,磁场![]() 的方向与圆柱的轴平行,在图中垂直纸平面向外.将半径也为
的方向与圆柱的轴平行,在图中垂直纸平面向外.将半径也为![]() 的光滑绝缘细环固定在纸平面上,并正好套住磁场区.在细环上串有一个质量为
的光滑绝缘细环固定在纸平面上,并正好套住磁场区.在细环上串有一个质量为![]() 、电量为
、电量为![]() (
(![]() )的带电小珠.设
)的带电小珠.设![]() 时,磁场
时,磁场![]() ,小珠在环上静止;
,小珠在环上静止;![]() 时,
时,![]() 随时间
随时间![]() 均匀地增长:
均匀地增长:![]() 时,
时,![]() ;
;![]() 时,
时,![]() 不变.试定量地讨论
不变.试定量地讨论![]() 时小珠的运动状态以及小珠对圆环的正压力(沿图中径向).设图中纸平面为水平面,小珠所受重力与环的支持力抵消.
时小珠的运动状态以及小珠对圆环的正压力(沿图中径向).设图中纸平面为水平面,小珠所受重力与环的支持力抵消.
【答案】在![]() 时间内,小珠对圆环的正压力为
时间内,小珠对圆环的正压力为![]() 。当
。当![]() 时。小珠对圆环的正压力为
时。小珠对圆环的正压力为![]()
【解析】
无限长圆柱形区域内匀强磁场随时间的变化产生涡旋电场,其电场线是以圆柱中央轴为圆心的一系列同心圆,固定细环所在处就是涡旋电场的电场线,串在细环上的带电小珠将受涡旋电场作用.涡旋电场对带电小珠的作用力沿细环切向,使小珠获得切向加速度,于是小珠绕细环做圆周运动的速度逐渐增大.随着小珠绕细环的运动,小珠还将受到磁场的洛仑兹力(其方向沿径向指向环心)以及细环的作用力(其方向也沿径向,由环心外指),两者的矢量和为小珠绕细环的圆周运动提供所需的向心力.所求小珠对细环的正压力正是上述细环对小珠作用力的反作用力.由已知条件,在![]() 时间内,磁场
时间内,磁场![]() 随时间
随时间![]() 线性地增长,且
线性地增长,且![]() 时
时![]() ,
,![]() 时
时![]() ,故有
,故有![]() .在此时间内,
.在此时间内,![]() 随
随![]() 的变化率为
的变化率为![]() .
.
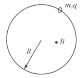
磁场的变化产生了涡旋电场![]() ,其电场线是一系列以圆柱中央轴为圆心的同心圆.由楞次定律,涡旋电场的圆形电场线为顺时针方向,故小珠所在处
,其电场线是一系列以圆柱中央轴为圆心的同心圆.由楞次定律,涡旋电场的圆形电场线为顺时针方向,故小珠所在处![]() 的方向如图所示.
的方向如图所示.
![]() 的大小的
的大小的
![]()
由此,小珠受到的沿环切向的涡旋电场的作用力为
![]() ,
,
相应的切向加速度为![]() .
.
因小珠在![]() 静止,故在
静止,故在![]() 时刻绕环做圆周运动的速度
时刻绕环做圆周运动的速度![]() .
.
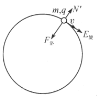
当小珠在![]() 时刻以
时刻以![]() 绕环运动时,所受磁场的洛仑兹力
绕环运动时,所受磁场的洛仑兹力![]() 指向圆心(如图所示),其大小为
指向圆心(如图所示),其大小为
![]() .
.
同时,小珠还受到细环的作用力![]() (方向见图),
(方向见图),![]() 与
与![]() 的矢量和提供了小珠绕环以
的矢量和提供了小珠绕环以![]() 运动所需的向心力
运动所需的向心力![]() (指向环心),其大小为
(指向环心),其大小为
![]() .
.
可见,![]() 的一半提供为向心
的一半提供为向心![]() ,另一半被
,另一半被![]() 抵消(故
抵消(故![]() 的方向必由环心外指),即
的方向必由环心外指),即![]() .
.
小珠对细环的正压力![]() 是
是![]() 的反作用力,故
的反作用力,故![]() 的方向沿径向指向圆心,大小为
的方向沿径向指向圆心,大小为![]() .
.
当![]() 时,
时,![]() 保持恒定,故涡旋电场不再存在
保持恒定,故涡旋电场不再存在![]() ,切向加速度随之消失,此时小珠将绕细环做匀速圆周运动,其速度
,切向加速度随之消失,此时小珠将绕细环做匀速圆周运动,其速度![]() .
.
此时小珠所受的洛仑兹力为(在上述![]() 公式中取
公式中取![]() )
)![]() .
.
此时小珠所需的向心力为(在![]() 的公式中取
的公式中取![]() ,
,![]() )
)
![]() .
.
可见,![]() 仍有一半被抵消,同样
仍有一半被抵消,同样![]() 仍成立,故
仍成立,故![]() .
.
在电磁感应现象中,若以导体为载体,则计算的多为感应电动势,同时伴随电路问题的研究;而撇开导体,研究的往往是感生电场,同时伴随着带电粒子在电场作用下的运动,而这种运动又是以洛仑兹力为背景的.
感生电动势与感生电场既相关联,又有差别,读者应注意对这两类问题进行专题分析与研究,熟练甄别其不同之处.

【题目】阅读材料,完成下列问题。
材料一:福建是我国海岸线最曲折的省区之一,沿海滩涂湿地资源丰富。下图为福建省及三沙湾区域示意图。

材料二:下表为 1971-2016 年三沙湾地区的风情统计表。
项目 | 1月 | 2月 | 3月 | 4月 | 5月 | 6月 | 7月 | 8月 | 9月 | 10月 | 11月 | 12月 |
平均风速(m/s) | 5.4 | 5.3 | 4.7 | 4.3 | 4.1 | 4.7 | 4.8 | 4.3 | 4.8 | 6.1 | 6.2 | 5.7 |
最大风速(m/s) | 18.0 | 16.0 | 18.0 | 16.0 | 15.3 | 17.7 | 26.5 | 25.0 | 29.0 | 22.5 | 19.0 | 18.0 |
同时风向 | NNE | NNE | ENE | NNE | SSW | SSE | NE | S | N | NNE | NNE | NNE |
最多风向 | NNE | NNE | NNE | NNE | NNE | SSW | SSW | SSW | NE | NNE | NNE | NNE |
风向频率(%) | 46 | 41 | 31 | 22 | 24 | 23 | 27 | 19 | 28 | 46 | 49 | 4 |
(说明:NNE 表示是北偏东北风,SSE 表示南偏东南风。)
材料三:图中所示海峡西岸经济区是指福州、厦门为中心,以闽东南为主体,北起浙江温州,南至广东汕头,向西延伸到南平、三明、龙岩的台湾海峡西部海域与陆地。该经济区重视台湾与大陆协作,注重打造的“环境友好型”工业区。
(1)简析三沙湾沿海滩涂丰富的主要成因。
(2)简述三沙地区年内盛行风向及风速特征的季节差异,并从气压和下垫面角度简析其成因。
(3)简析福建发展风电产业的有利和限制条件。
(4)从地理位置角度分析海西经济区的主要区位优势,并从“环境友好型”角度指出该经济区引入的工业项目应具备的基本要求。