题目内容
【题目】如图甲所示，静止的圆锥体竖直放置，顶角为
，质量为
，且分布均匀的链条水平地套在圆锥体上，忽略链条与锥面之间的摩擦力，试求链条中的张力.
【答案】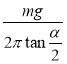
【解析】
由对称性易知，链条内部各处的张力应是处处相等的，而要求链条内部的张力，则需将链条内部的张力转化为外力，这就需要从链条中隔离出某一部分作为研究对象，在本题中，可取一小段
为研究对象，即中学阶段常用的微元法.
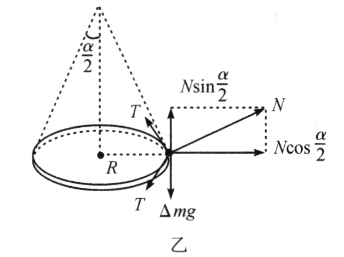
如图乙所示，设链条环半径为
，在链条环中任取一小段
为研究对象，设其质量为
，受力为：圆锥面的支持力
，其方向垂直于圆锥面，重力
以及两端所受的张力
。平衡时上述诸力在水平面的分力之和为零，在铅垂方向的分力之和也应为零。据此，列出相应的两个方程，即可解出.
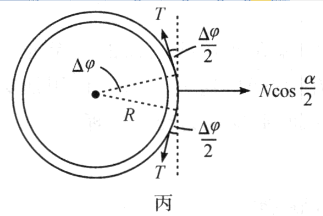
如图丙所示，圆锥面支持力在水平面内的分力为
，它与小段两端所受张力应达到平衡。设对链条环中心的张角为
，在水平方向的受力如图丙所示，则有
. ①
因很短，很小，故有
. ②
将②代入①，得
. ③
又在铅垂方向亦应受力平衡，故有
. ④
由以上两式得
， ⑤
式中
. ⑥
将⑥代入⑤，得
.
故链条环中的张力为
.
练习册系列答案
相关题目
