题目内容
【题目】如图所示，在xOy平面第一象限内的某区域有垂直平面匀强磁场（没画出），一个质量为m、电荷量为q的电带粒子。由y轴上的P点开始运动，初速度为v0 ， 方向沿x轴正方向；P到O的距离为 
；后来，粒子经过x轴上的Q点，此时速度方向与x轴负方向的夹角为θ=60°，Q到O的距离为2L，磁场的磁感应强度 
。
（1）求带电粒子从P点运动到Q点所用的时间；
（2）若匀强磁场的区域是圆形磁场，求圆形磁场的最小面积；
（3）若匀强磁场的区域是矩形，求矩形磁场的最小面积。
【答案】
（1）
带电粒子的运动轨迹如图所示，M点是进磁场的点，N点是出磁场的点。
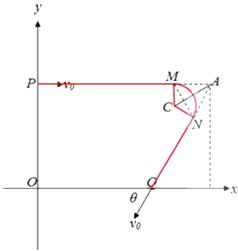
带电粒子在匀强磁场中做匀速圆周运动的向心力由洛伦兹力提供
，解得带电粒子做匀速圆周运动的半径 
由几何关系得：A点坐标（3L， 
）；PM= 
；NQ= 
；∠MCN= 
带电粒子从P点运动到Q点所用的时问， 
（2）
若匀强磁场的区域是圆形磁场，以MN为直径的圆的面积最小，如下图所示。
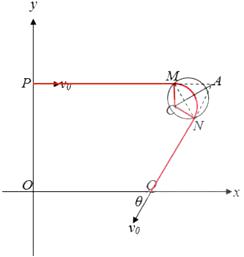
由几何关系可得: 
（3）
若匀强磁场的区域是矩形，矩形以 MN 为边长，MN 的对边与圆形相切的矩形面积最小，如图所示
最小矩形的面积 
【解析】（1）根据粒子做圆周运动的周期公式与转过的圆心角求出粒子的运动时间，然后求出离开磁场的运动时间，再求出总的运动时间．（2）求出磁场的最小半径，然后求出最小面积；（3）矩形的最小面积应恰好包含粒子的运动轨迹，求出矩形的长、宽，也就求出了矩形的最小面积．
练习册系列答案
相关题目
