Question

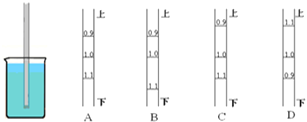
【题目】三个完全相同的长方体木块，把它们分别放在三种密度不同的液体里，木块静止时浸入液体的情况是：甲木块大部分浸入；乙木块一半浸入；丙木块小部分浸入，如图所示。若将三木块露出液面部分切除后，剩下部分分别放入原容器中，则木块露出液面部分的体积

A. 甲最多 B. 乙最多 C. 丙最多 D. 一样多

Answer 1

【答案】B

【解析】

（1）物体漂浮时，露出液面部分的体积占总体积的比例是由物体的密度和液体的密度共同决定的，物体和液体的密度不变，露出液面部分的体积占总体积的比例也不变。

（2）因为甲木块大部分浸入；乙木块一半浸入；丙木块小部分浸入，所以可以假设甲木块有的体积浸入；乙木块有的体积一半浸入；丙木块有的体积浸入。

设长方体木块的体积为V，则将木块露出液面的部分切除后：

图中甲木块的体积为V浸入，木块再次露出液面部分的体积仍为现有体积的，即V甲＝V×＝V。

图中乙木块的体积为V浸入，木块再次露出液面部分的体积仍为现有体积的，即V乙＝V×＝V。

图中丙木块的体积为V浸入，木块再次露出液面部分的体积仍为现有体积的，即V丙＝V×＝V。

因为V＞V，所以乙图木块再次露出液面部分的体积较大。

故选：B。