题目内容
【题目】林丹最喜爱的用于锻炼臂力的健身拉力器结构示意图如图所示,他用250N的拉力向下拉动杠杆,使20kg的配重块在0.4s内匀速升高了40cm,脱不计拉杆和绳的重力,g取10N/kg,求:
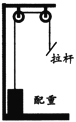
(1)林丹拉动拉力器的功率.
(2)林丹拉动拉力器过程中克服摩擦所做的功.
(3)在此过程中拉力器的机械效率.
【答案】(1)林丹拉动拉力器的功率为250W;
(2)林丹拉动拉力器过程中克服摩擦所做的功为20J;
(3)在此过程中拉力器的机械效率为80%
【解析】
试题分析:(1)图中两个滑轮均为定滑轮,绳端移动的距离和配重上升的高度相同,根据W=Fs求出拉力做的功,根据P=![]() 求出拉动拉力器的功率;
求出拉动拉力器的功率;
(2)知道配重的质量和上升的高度,根据W=Gh=mgh求出有用功,总功和有用功的差值即为克服摩擦所做的功;
(3)根据η=![]() ×100%求出此过程中拉力器的机械效率.
×100%求出此过程中拉力器的机械效率.
解:(1)拉力做的功:
W总=Fs=Fh=250N×40×10﹣2m=100J,
拉动拉力器的功率:
P=![]() =
=![]() =250W;
=250W;
(2)拉力做的有用功:
W有=Gh=mgh=20kg×10N/kg×40×10﹣2m=80J,
拉动拉力器过程中克服摩擦所做的功:
W额=W总﹣W有用=100J﹣80J=20J;
(3)此过程中拉力器的机械效率:
η=![]() ×100%=
×100%=![]() ×100%=80%.
×100%=80%.
答:(1)林丹拉动拉力器的功率为250W;
(2)林丹拉动拉力器过程中克服摩擦所做的功为20J;
(3)在此过程中拉力器的机械效率为80%.

练习册系列答案
相关题目

