题目内容
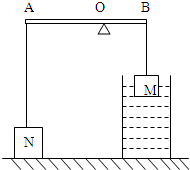如图所示装置中，O为轻质杠杆AB的支点，AO：OB=3：2，A端用细绳连接一个质量为3kg放在水面地面上的物体N，B端用细绳悬挂一质量为2kg的物体M，物体M有3/5的体积露出水面，此时杠杆恰好在水平位置平衡．已知物体M的体积为500cm3．g取10N/kg，绳子的质量忽略不计．求：地面对物体N的支持力．分析：由浮力公式求出M受到的浮力，然后求出杠杆在B端受到的拉力，由杠杆平衡条件求出杠杆在A端受到的拉力；最后求出地面对N的支持力．
解答：解：M受到的浮力F浮=ρ水gV排=1×103kg/m3×10N/kg×（1-
）×500×10-6m3=2N，
杠杆B端受到的拉力FB=GM-F浮=mMg-F浮=2kg×10N/kg-2N=18N，
由杠杆平衡条件得：FA×AO=FB×OB，
则FA=
=18N×
=12N，
地面对N的支持力F=GN-FA=mNg-FA=3kg×10N/kg-12N=18N；
答：地面对物体N的支持力18N．
| 3 |
| 5 |
杠杆B端受到的拉力FB=GM-F浮=mMg-F浮=2kg×10N/kg-2N=18N，
由杠杆平衡条件得：FA×AO=FB×OB，
则FA=
| FB×OB |
| AO |
| 2 |
| 3 |
地面对N的支持力F=GN-FA=mNg-FA=3kg×10N/kg-12N=18N；
答：地面对物体N的支持力18N．
点评：对物体进行受力分析，应用浮力公式、杠杆平衡条件即可正确解题，本题有一定难度．
练习册系列答案
七星图书口算速算天天练系列答案
相关题目
（2012?顺义区二模）如图所示装置中，杠杆和滑轮的重力及滑轮的摩擦均可忽略不计，杠杆AB可以绕O点在竖直平面内自由转动，A端通过竖直方向的轻绳与滑轮组相连，在B端用一轻绳沿竖直方向将杠杆拉住，使其始终保持水平平衡．在滑轮组的下方，悬挂一圆柱形的物体，此物体被浸在圆柱形容器内的液体中．已知杠杆O点两侧的长度关系为AO=2OB，圆柱形物体的底面积为10cm2、高为12cm，圆柱形容器的底面积为50cm2．若容器中的液体为水，在水深为20cm时物体的上表面恰与水面相平，此时杠杆B端绳上的拉力为F1；打开圆柱形容器下方的阀门K，将水向外释放，直到物体露出水面的体积为其总体积的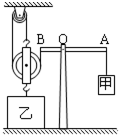
在如图所示装置中，甲物重G甲=10N，乙物重G乙是动滑轮重G轮的8倍．物体乙跟地面的接触面积为1.5×10-2m2．轻杆AB可以绕O点转动，且OA：OB=2：1．不计轴摩擦，装置如图所示处于平衡状态时，乙对水平地面的压强p=2×103Pa．乙物体所受的重力
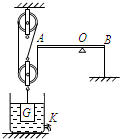（2011?怀柔区二模）如图所示装置中，杠杆和滑轮的重力及滑轮的摩擦均可忽略不计，杠杆AB可以绕O点在竖直平面内自由转动，A端通过竖直方向的轻绳与滑轮组相连，在B端用一轻绳沿竖直方向将杠杆拉住，使其始终保持水平平衡．在滑轮组的下方，悬挂一圆柱形的物体，此物体被浸在圆柱形容器内的液体中．已知杠杆O点两侧的长度关系为AO=2OB，圆柱形物体的底面积为10cm2、高为12cm，圆柱形容器的底面积为50cm2．若容器中的液体为水，在水深为20cm时物体的上表面恰与水面相平，此时杠杆B端绳上的拉力为F1；打开圆柱形容器下方的阀门K，将水向外释放，直到物体露出水面的体积为其总体积的2/3时，将阀门K关闭，此时杠杆B端绳上的拉力为F2，且F1：F2=3：5．若容器中液体为某种未知液体，其质量与最初容器中的水的质量相等，此时未知液体的深度为18cm，杠杆B端绳上的拉力为F3．（取g=10N/kg）
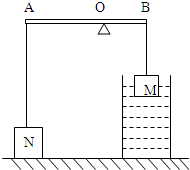如图所示装置中，O为轻质杠杆AB的支点，AO：OB=3：2，A端用细绳连接一个质量为3kg放在水面地面上的物体N，B端用细绳悬挂一质量为2kg的物体M，物体M有3/5的体积露出水面，此时杠杆恰好在水平位置平衡．已知物体M的体积为500cm3．g取10N/kg，绳子的质量忽略不计．求：地面对物体N的支持力．