题目内容
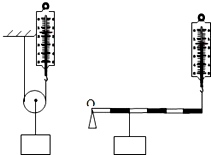 (2013?孝南区一模)小红同学用如图所示的两种机械做了探究“使用机械是否能省功”的实验,得到下表中的数据.
(2013?孝南区一模)小红同学用如图所示的两种机械做了探究“使用机械是否能省功”的实验,得到下表中的数据.| 次数 | 使用机械 | 钩码重/N | 钩码上升的距离/m | 弹簧测力计的示数/N | 弹簧测力计作用点移动距离/m | W有用功/J | W总/J |
| 1 | 动滑轮 | 1 | 0.10 | 0.6 | 0.20 | 0.10 | 0.12 |
| 2 | 动滑轮 | 2 | 0.20 | 1.1 | 0.40 | 0.40 | 0.44 |
| 3 | 杠杆 | 1 | 0.05 | 0.4 | 0.15 | 0.06 | |
| 4 | 杠杆 | 2 | 0.10 | 0.7 | 0.30 | 0.20 | 0.21 |
0.05
0.05
J,机械效率是83.3%
83.3%
(保留一位小数).(2)比较落后2、4次实验,机械效率大的是
第4次实验
第4次实验
(3)分析实验田1、2的数据还可初步得出有关动滑轮机械效率与钩码重量的关系是:
物体越重,机械效率越高
物体越重,机械效率越高
. (4)请在杠杆机械中画出重物所受重力的示意图和拉力的力臂.
分析:(1)根据公式W=Gh求出有用功,根据η=
求出机械效率;
(2)根据η=
求出两次实验中的机械效率,然后进行比较;
(3)根据η=
求出两次实验中的机械效率,然后得出结论;
(4)重力的示意图画法:找出物体的重心,从重心开始画一个竖直向下的箭头;动力臂即支点到动力作用线的距离.
| W有用 |
| W总 |
(2)根据η=
| W有用 |
| W总 |
(3)根据η=
| W有用 |
| W总 |
(4)重力的示意图画法:找出物体的重心,从重心开始画一个竖直向下的箭头;动力臂即支点到动力作用线的距离.
解答:解:(1)第3次实验中,有用功W有用=Gh=1N×0.05m=0.05J;总功W总=0.06J,所以其机械效率η3=
×100%=
×100%≈83.3%;
(2)第2次实验中,其机械效率η2=
×100%=
×100%≈90.9%;
第4次实验中,其机械效率η4=
×100%=
×100%≈95.2%,
所以第4次实验中的机械效率大;
(3)第1次实验中,其机械效率η1=
×100%=
×100%≈83.3%,
综上所述,第2次实验中的机械效率大于第1次的机械效率,所以动滑轮机械效率与钩码重量的关系是:物体越重,机械效率越高;
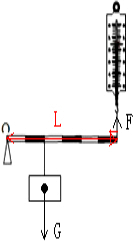
(4)形状规则、质地均匀的物体,它的重心在它的几何中心上,重力方向是竖直向下的,如下图;
O点为支点,过O点作垂直于拉力F作用线的垂线L,即为拉力的力臂,如下图;
| W有用 |
| W总 |
| 0.05J |
| 0.06J |
(2)第2次实验中,其机械效率η2=
| W有用 |
| W总 |
| 0.40J |
| 0.44J |
第4次实验中,其机械效率η4=
| W有用 |
| W总 |
| 0.20J |
| 0.21J |
所以第4次实验中的机械效率大;
(3)第1次实验中,其机械效率η1=
| W有用 |
| W总 |
| 0.10J |
| 0.12J |
综上所述,第2次实验中的机械效率大于第1次的机械效率,所以动滑轮机械效率与钩码重量的关系是:物体越重,机械效率越高;
(4)形状规则、质地均匀的物体,它的重心在它的几何中心上,重力方向是竖直向下的,如下图;
O点为支点,过O点作垂直于拉力F作用线的垂线L,即为拉力的力臂,如下图;

点评:此题主要考查的是学生对功、机械效率的计算公式的理解和掌握,以及力的示意图的画法,要注意力的作用点和方向;同时考查了力臂的画法,基础性题目.

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目
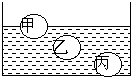 (2013?孝南区一模)甲乙丙三小球质量相同,放入水中后,甲漂浮,乙球悬浮,丙球下沉,位置如图,则( )
(2013?孝南区一模)甲乙丙三小球质量相同,放入水中后,甲漂浮,乙球悬浮,丙球下沉,位置如图,则( )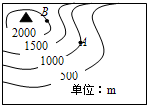 (2013?孝南区一模)如图所示为一高山的等高图,某登山运动员从A点到B点过程中,下列说法正确的是( )
(2013?孝南区一模)如图所示为一高山的等高图,某登山运动员从A点到B点过程中,下列说法正确的是( )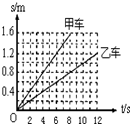 (2013?孝南区一模)甲乙两小车同时同地向做匀速直线运动,它们的s-t图象如图所示.经过6秒,此段时间内,下列说法正确的是( )
(2013?孝南区一模)甲乙两小车同时同地向做匀速直线运动,它们的s-t图象如图所示.经过6秒,此段时间内,下列说法正确的是( )