Question

流量表示单位时间内通过某一横截面的流体的体积，用字母Q表示，定义式为Q=

V

t

．
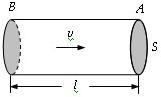
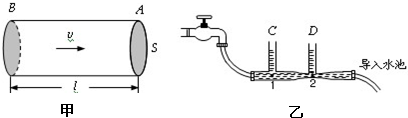
（1）如图1所示，水流在粗细均匀的水平管道内向右匀速流动，设水流速度为v，管内通道的横截面积为S．取一段管道AB，水从A端流到B端所用时间为t，则AB间水柱的体积V=

 

（要求用S、v、t表示），据定义可导出流量又可表示为 Q=

 

．
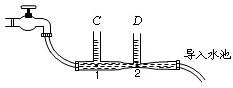
（2）如图2所示的连通器，当阀门K关闭时，C、D两竖直细玻璃管中液面相平．打开阀门K，待水流稳定后，比较C、D玻璃管中的水面高度，

 

管中的水面较高．

Answer 1

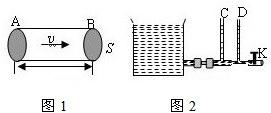
分析：（1）已知水流的速度和流动的时间，根据公式S=vt可求水流过的路程，还知管道的横截面积，可求水柱的体积，
已知Q=

V

t

，把体积表达式代入，可求流量的表达式．
（2）D管比C管的横截面积小，横截面积越小，水流动速度快，产生的压强小，横截面积大，水流动速度慢，产生的压强大，能支持的水柱就越高．

解答：解：（1）水在管道内流过的距离h=vt，所以水柱的体积V=Sh=Svt，
因为Q=

V

t

，所以Q=

Svt

t

=Sv．
（2）C管横截面积大，水流动速度慢，产生的压强大，能支持的水柱就高，所以C管水面高．
故答案为：Svt；Sv；C．

点评：本题考查水流量表达式的推导和流体压强与流速的关系，关键知道，水流动速度越快，产生的压强越小．