题目内容
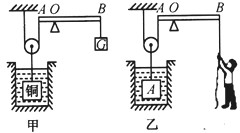
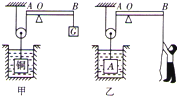 如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求:
如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求:
(1)此装置中动滑轮的重G动;
(2)小明所能吊起物块A的最大质量mA.
解:(1)由杠杆平衡条件得:FA×OA=GB×OB,则FA=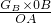 =
= =336N,
=336N,
由平衡条件得:(ρ铜-ρ水)Vg+G动=2FA,G动=2FA-(ρ铜-ρ水)Vg=2×336N-(8.9×103kg/m3-1×103kg/m3)×(0.2m)3×10N/kg=40N;
(2)小明的最大拉力F=G=mg=40kg×10N/kg=400N,
由杠杆平衡条件得:F最大×OA=F×OB,即F最大×OA=400N×3OA,F最大=1200N;
由平衡条件得:G-ρ水VAg+G动=2F最大,G=2F最大+ρ水VAg-G动=2×1200N+1×103kg/m3×0.040m3×10N/kg-40N=1560N,
∵G=mg,∴物体的质量m=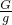 =
= =156kg;
=156kg;
答:(1)此装置中动滑轮的重为40N;
(2)小明所能吊起物块A的最大质量为156kg.
分析:(1)由杠杆平衡条件求出A端绳子对杠杆的拉力,由密度公式的变形公式、浮力公式及平衡条件可以求出动滑轮的重力.
(2)小明对B端的最大拉力等于其重力,由杠杆平衡条件求出A端的最大拉力,然后求出A的最大重力,最后求出A的质量.
点评:本题考查了杠杆平衡条件的应用、浮力公式、密度公式的变形公式的应用,对物体正确受力分析、应用杠杆平衡条件、力的平衡条件,即可正确解题.
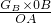 =
= =336N,
=336N,由平衡条件得:(ρ铜-ρ水)Vg+G动=2FA,G动=2FA-(ρ铜-ρ水)Vg=2×336N-(8.9×103kg/m3-1×103kg/m3)×(0.2m)3×10N/kg=40N;
(2)小明的最大拉力F=G=mg=40kg×10N/kg=400N,
由杠杆平衡条件得:F最大×OA=F×OB,即F最大×OA=400N×3OA,F最大=1200N;
由平衡条件得:G-ρ水VAg+G动=2F最大,G=2F最大+ρ水VAg-G动=2×1200N+1×103kg/m3×0.040m3×10N/kg-40N=1560N,
∵G=mg,∴物体的质量m=
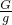 =
= =156kg;
=156kg;答:(1)此装置中动滑轮的重为40N;
(2)小明所能吊起物块A的最大质量为156kg.
分析:(1)由杠杆平衡条件求出A端绳子对杠杆的拉力,由密度公式的变形公式、浮力公式及平衡条件可以求出动滑轮的重力.
(2)小明对B端的最大拉力等于其重力,由杠杆平衡条件求出A端的最大拉力,然后求出A的最大重力,最后求出A的质量.
点评:本题考查了杠杆平衡条件的应用、浮力公式、密度公式的变形公式的应用,对物体正确受力分析、应用杠杆平衡条件、力的平衡条件,即可正确解题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
 (2010?宣武区二模)如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求:
(2010?宣武区二模)如图甲所示的装置中,轻质杠杆AB可绕0点在竖直平面内转动,3AO=OB,一个边长 为20cm的正方体铜块完全浸没在水中,当在杠杆右端用细钢丝挂重为112N的重物G时,杠杆AB恰处于水平平衡;若利用此装置提拉一个物块A,质量为40Kg的小明用力拉住杠杆B端使杠杆水平平衡,如图乙所示.已知物块A的体积为40dm3.若杠杆的质量、细钢丝的质量与摩擦均忽略不计(g取10N/Kg,ρ铜=8.9g/cm3).求: