题目内容
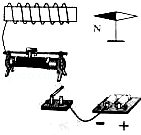
如图为一台两挡式电热水器的内部简化电路,S为温控开关,当S接a时电路中的电流为5A;当S接b时电路消耗的电功率为22W.求: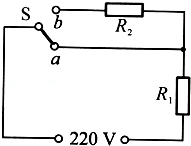
(1)R1的电阻;
(2)高温挡时电路消耗的电功率;
(3)在低温挡工作l0min,电流通过R2产生的热量.
(1)R1的电阻为44Ω;
(2)高温挡时电路消耗的电功率为1100W;
(3)在低温挡工作l0min,电流通过R2产生的热量为12936J
解析试题分析:(1)当S接a时,电路为R1的简单电路,此时电路中的总电阻最小,根据P=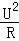 可知,电热水器处于高温档位,根据欧姆定律求出R1的电阻;
可知,电热水器处于高温档位,根据欧姆定律求出R1的电阻;
(2)根据P=UI求出高温挡时电路消耗的电功率;
(3)当S接b时,两电阻串联,电路中的总电阻最大,电功率最小处于低温档位,根据P=UI求出电路中的电流,根据欧姆定律求出电路中的总电阻,利用电阻的串联求出R2的阻值,再根据Q=I2Rt求出工作l0min电流通过R2产生的热量.
(1)当S接a时,电路为R1的简单电路,电热水器处于高温档位,
根据欧姆定律可得:
R1=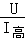 =
= =44Ω;
=44Ω;
(2)高温挡时电路消耗的电功率:
P高=UI高=220V×5A=1100W;
(3)当S接b时,两电阻串联,电热水器处于低温档位,电路中的电流:I低=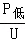 =
=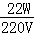 =0.1A,
=0.1A,
电路中的总电阻:R总=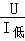 =
=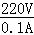 =2200Ω,
=2200Ω,
∵串联电路中总电阻等于各分电阻之和,
∴R2=R总﹣R1=2200Ω﹣44Ω=2156Ω,
工作l0min电流通过R2产生的热量:
Q2=I低2R2t=(0.1A)2×2156Ω×10×60s=12936J.
考点:电功率的计算;欧姆定律的应用;电阻的串联;焦耳定律的计算公式及其应用
点评:本题考查了电阻的串联和欧姆定律、焦耳定律、电功率公式的应用,关键是结合电路图判断高温档位和低温档位

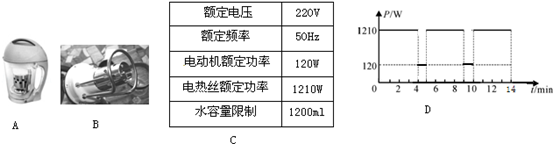
某中学为解决同学们的饮水问题,新购置了一批台式饮水机,其铭牌如下表所示.图是饮水机的电路图,S是用感温材料制造的温控开关,R1是电阻,R2是供加热的电阻丝.分析电路图可知,当S接通时,饮水机处于加热状态,当S断开时处于保温状态。
| 额定频率 | 50Hz | 环境温度 | 10℃~38℃ |
| 加热功率 | 550W | 环境湿度 | ≤90% |
| 额定电压 | 220V | 制热水能力 | ≥90℃ 5L/h |

(1)在加热状态下,饮水机正常工作时电路中的电流是多大?
(2)正常工作时该饮水机将热水罐中0.6kg,l8℃的水加热到93℃,用时6min。用这些数据及题目中的信息,计算热水罐中的水吸收的热量和该饮水机加热状态时的效率。[C水=4.2×103J /(kg·℃)]
(3)如果要使饮水机在保温状态时的功率是加热状态时的一半,则R1与R2的比值应是多少?
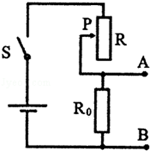
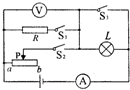
小华用如图所示的电路测小灯泡功率.电路中电源电压恒为4.5V,电压表的量程为O~3V,电流表的量程为0~0.6A,滑动变阻器的规格为“20Ω 1A”,灯泡标有“2.5V 1.25W”字样.若闭合开关,两电表的示数均不超过所选量程,灯泡两端电压不允许超过额定值,不考虑灯丝电阻的变化,则下列说法正确的是( )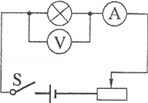
| A.电流表示数的变化范围是O~0.5A |
| B.滑动变阻器的电阻允许调节的范围是2.5~20Ω |
| C.灯泡的最小功率是0.162W |
| D.该电路的最大功率是2.7W |
小丽在观察小提琴、二胡、贝司等弦乐器的弦振动时猜想:即使在弦张紧相同的条件下发声的音调高低也可能与弦的粗细、长度及弦的材料有关。于是,她通过实验来探究一下自己的猜想是否正确,下表是她在实验时控制的琴弦条件:
| 编号 | 材料 | 长度/cm | 横截面积/m2 |
| 1 | 铜 | 60 | 0.76 |
| 2 | 铜 | 80 | 0.76 |
| 3 | 铜 | 100 | 0.76 |
| 4 | 铜 | 80 | 1.02 |
| 5 | 尼龙 | 80 | 1.02 |
| 6 | 尼龙 | 100 | 1.02 |
(1)如果小丽想探究发声的音调与弦的粗细的关系,你认为应选用表中的编号为
的琴弦。(只填数字序号)
(2)探究过程通常采用下列的一些步骤:A、分析归纳 B、实验研究 C、提出问题(或猜想)D、得出结论
你认为小丽要完成本探究的全过程,所采取步骤的合理顺序应该是: (只填字母序号)
(3)如果小丽想探究发声的音调与琴弦的材料关系,你认为应选用表中的编号为
的琴弦。(只填数字序号)
(4)在上述探究过程中,总要控制某些因素不变,来找出另外一些因素的关系,这种科学的方法叫做 。