题目内容
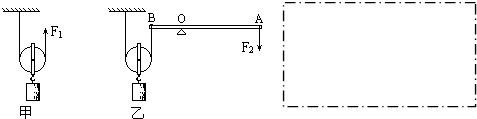
在生产中,人们往往用的是由杠杆、滑轮等简单机械组合而成的复杂机械.在一次综合实践活动中,王刚同学分别用一轻质杠杆(O为支点,OA=3OB)、一只滑轮和一些细绳构成的组合机械来提升重90N的物体.王刚在实践活动中是这样做的:他先单独使用一个动滑轮来提升重物如图甲所示,然后又用动滑轮和杠杆组成的组合机械来提升重物,如图乙所示.
(1)在不计机械重,绳重,部件间摩擦时,F1=________N,F2=________N.比较F1、F2可以看出,使用乙图组合机械的好处是________.
(2)请你帮他设计出一种能省距离的组合机械,请把设计方案图画在下面的方框内.
(3)王刚在实验中突然提出这样一个问题,使用乙图的组合机械与使用甲图的动滑轮相比,它的机械效率是否发生改变呢?
㈠为了比较甲、乙两机械效率的大小,需要测量的量有:________.
㈡机械效率η甲=________,η乙=________.(用测量的量来表示)
解:(1)甲图拉力是重力的一半,F1=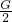 =
=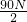 =45N,
=45N,
乙图中F1?OB=F2?OA,
所以F2=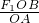 =
=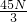 =15N.
=15N.
很明显45N>15N,所以使用乙图组合机械的好处是可以更加省力.
故答案为:45,15,可以更加省力.
(2)使杠杆的阻力臂大于动力臂,即可改为能省距离的组合机械.如图:
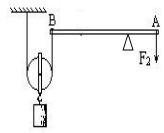
(3)第一步先测出甲图中物体升高的高度h和绳子自由端移动的距离S1,
第二步测出物体升高的高度h和拉力向下移动的距离S2,
第三步根据公式根据公式η= 得出机械效率的大小.
得出机械效率的大小.
图甲中,由于定滑轮不省力,所以F1=G;
η甲=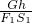 =
=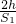 .
.
图乙中,在不计绳重、摩擦和动滑轮重的情况下,由动滑轮的工作特点和杠杆的平衡条件得:
F2?OA=FB?OB,而FB= G,即F2?OA=
G,即F2?OA= G?OB,由于OA=3OB,所以G=6F2;
G?OB,由于OA=3OB,所以G=6F2;
η乙=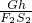 =
=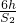 .
.
故答案为:物体提升的高度和拉力移动的距离;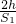 ;
;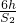 .
.
分析:(1)甲图动滑轮上有两端绳子,拉力是重力的一半,乙图中,已知动滑轮上拉力的大小,根据杠杆平衡条件F1L1=F2L2,可求拉力F2的大小.比较两拉力的大小,就可得出使用乙图组合机械的好处,
(2)乙图设计的是省力的组合机械,减小杠杆的动力臂,增大杠杆的阻力臂,即可改为能省距离的组合机械.
(3)已知物体的重力和拉力的大小,分别把重物提升相同的高度,再测出拉力移动的距离,根据公式η= 即可得出两装置的机械效率.
即可得出两装置的机械效率.
点评:本题考查滑轮组绳子拉力的计算和机械效率的计算以及滑轮组的设计与组装,关键是根据杠杆的平衡条件求拉力的大小,难点是设计省距离的组合机械.
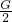 =
=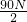 =45N,
=45N,乙图中F1?OB=F2?OA,
所以F2=
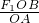 =
=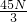 =15N.
=15N.很明显45N>15N,所以使用乙图组合机械的好处是可以更加省力.
故答案为:45,15,可以更加省力.
(2)使杠杆的阻力臂大于动力臂,即可改为能省距离的组合机械.如图:

(3)第一步先测出甲图中物体升高的高度h和绳子自由端移动的距离S1,
第二步测出物体升高的高度h和拉力向下移动的距离S2,
第三步根据公式根据公式η=
 得出机械效率的大小.
得出机械效率的大小.图甲中,由于定滑轮不省力,所以F1=G;
η甲=
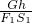 =
=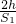 .
.图乙中,在不计绳重、摩擦和动滑轮重的情况下,由动滑轮的工作特点和杠杆的平衡条件得:
F2?OA=FB?OB,而FB=
 G,即F2?OA=
G,即F2?OA= G?OB,由于OA=3OB,所以G=6F2;
G?OB,由于OA=3OB,所以G=6F2;η乙=
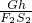 =
=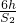 .
.故答案为:物体提升的高度和拉力移动的距离;
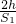 ;
;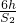 .
.分析:(1)甲图动滑轮上有两端绳子,拉力是重力的一半,乙图中,已知动滑轮上拉力的大小,根据杠杆平衡条件F1L1=F2L2,可求拉力F2的大小.比较两拉力的大小,就可得出使用乙图组合机械的好处,
(2)乙图设计的是省力的组合机械,减小杠杆的动力臂,增大杠杆的阻力臂,即可改为能省距离的组合机械.
(3)已知物体的重力和拉力的大小,分别把重物提升相同的高度,再测出拉力移动的距离,根据公式η=
 即可得出两装置的机械效率.
即可得出两装置的机械效率.点评:本题考查滑轮组绳子拉力的计算和机械效率的计算以及滑轮组的设计与组装,关键是根据杠杆的平衡条件求拉力的大小,难点是设计省距离的组合机械.

练习册系列答案
相关题目
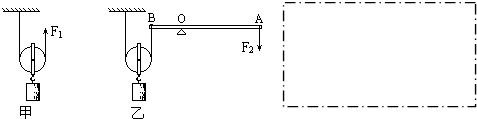
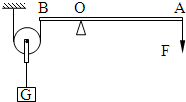 (2006?房山区一模)在生产中,人们往往用的是由杠杆、滑轮等简单机械组合而成的复杂机械.在一次科技活动中,某校物理小组的同学们分别用一轻质杠杆(不计杆重)、一只滑轮和一些细绳构成了如图所示的组合机械,其中O为支点,OA=3OB,他们发现使用组合机械可以更省力,如果提升G=90N的物体.在不计滑轮重、杆重和绳重及部件间的摩擦时,拉力F=
(2006?房山区一模)在生产中,人们往往用的是由杠杆、滑轮等简单机械组合而成的复杂机械.在一次科技活动中,某校物理小组的同学们分别用一轻质杠杆(不计杆重)、一只滑轮和一些细绳构成了如图所示的组合机械,其中O为支点,OA=3OB,他们发现使用组合机械可以更省力,如果提升G=90N的物体.在不计滑轮重、杆重和绳重及部件间的摩擦时,拉力F=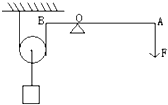 在生产中,人们往往用简单机械组合成复杂机械.在一次综合实践活动中,王刚同学用他做的组合机械来提升重物.如图,这个组合机械是由
在生产中,人们往往用简单机械组合成复杂机械.在一次综合实践活动中,王刚同学用他做的组合机械来提升重物.如图,这个组合机械是由
