题目内容
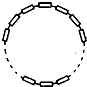 2n+1个阻值均为R的电阻通过导线首尾连成一圆环,相邻的两个电阻之间均可引出一接线柱,从而构成一变阻器,则利用该变阻器可获得不同阻值的个数为
2n+1个阻值均为R的电阻通过导线首尾连成一圆环,相邻的两个电阻之间均可引出一接线柱,从而构成一变阻器,则利用该变阻器可获得不同阻值的个数为分析:因为取不同接线柱时,相当于有两串电阻并联,而只要改变一个接线柱,就可以使两条支路上的阻值发生改变,从而影响到最终得到的并联后的总阻值的大小,从而实现了变阻.
解答:解:该变阻器可以得到的电路是一个电阻与2n个电阻并联、两个电阻与2n-1个电阻并联、…n个电阻与n+1个电阻并联,依此类推又为n个电阻与n+1个电阻并联、…两个电阻与2n-1个电阻并联、一个电阻与2n个电阻并联与前面重复,因此利用该变阻器可获得不同阻值的个数为n个;
当n个电阻与n+1个电阻并联时,阻值最大,即
=
.
故答案为:n;=
.
当n个电阻与n+1个电阻并联时,阻值最大,即
| nR×(n+1)R |
| nR+(n+1)R |
| n(n+1)R |
| 2n+1 |
故答案为:n;=
| n(n+1)R |
| 2n+1 |
点评:本题的关键点是知道变阻器的原理,知道各电阻的连接方式,最后根据并联电路电阻的特点分析计算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目

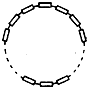 2n+1个阻值均为R的电阻通过导线首尾连成一圆环,相邻的两个电阻之间均可引出一接线柱,从而构成一变阻器,则利用该变阻器可获得不同阻值的个数为________个; 最大阻值为________.
2n+1个阻值均为R的电阻通过导线首尾连成一圆环,相邻的两个电阻之间均可引出一接线柱,从而构成一变阻器,则利用该变阻器可获得不同阻值的个数为________个; 最大阻值为________.