题目内容
 (2010?昌平区一模)如图所示,放在水平桌面上的容器甲为圆柱形,底面积为S1,容器乙下半部分为圆锥形,底面积为S1,上半部分为圆柱形,底面积为S2,S1:S2=2:1,甲、乙两容器的质量相等.如图所示甲、乙两容器装入深度相同的水后,再分别放入体积相同,密度不同的物块A和B,物块A放在容器甲中,静止时有
(2010?昌平区一模)如图所示,放在水平桌面上的容器甲为圆柱形,底面积为S1,容器乙下半部分为圆锥形,底面积为S1,上半部分为圆柱形,底面积为S2,S1:S2=2:1,甲、乙两容器的质量相等.如图所示甲、乙两容器装入深度相同的水后,再分别放入体积相同,密度不同的物块A和B,物块A放在容器甲中,静止时有| 1 |
| 3 |
| 1 |
| 4 |
分析:(1)由图可知放入物块前,甲中水的体积比乙中水的体积大,根据m=ρV和水平面上物体的压力和自身的重力相等可知两容器对桌面压力的关系;根据已知条件和F=Ps=ρghs可知两容器底部受到水的压力关系.
(2)放入物块后,根据露出水面的体积求出排开水的体积;根据物体排开液体的体积利用V=Sh求出液体深度的变化量,根据P=ρgh求出液体对容器底部压强的变化量,再利用F=Ps求出容器底部受到水的压力变化量,据此求出容器底部受到水的压力变化量之比.
(2)放入物块后,根据露出水面的体积求出排开水的体积;根据物体排开液体的体积利用V=Sh求出液体深度的变化量,根据P=ρgh求出液体对容器底部压强的变化量,再利用F=Ps求出容器底部受到水的压力变化量,据此求出容器底部受到水的压力变化量之比.
解答:解:(1)放入物块前,
∵甲中水的体积比乙中水的体积大,且m=ρV,
∴甲中水的质量比乙中水的质量大,
又∵水平面上物体的压力和自身的重力相等,m甲=m乙,
∴F甲>F乙;
∵两容器水的深度相同,底面积相同,
∴根据F=Ps=ρghs可知:甲、乙两容器底部受到水的压力相等.
(2)放入物块后,
V排A=(1-
)V=
V,V排B=(1-
)V=
V,
∴V排A:V排B=8:9;
液体上升的高度为△h=
,
液体对容器底部压强的变化量为△P=ρ水g△h=ρ水g
,
容器底部受到水的压力变化量△F=△Ps1=ρ水g
s1,
∴甲、乙容器底部受到水的压力变化量之比为:
△F甲:△F乙=
s1:
s1=
:
=
:
=
×
=4:9.
故选D.
∵甲中水的体积比乙中水的体积大,且m=ρV,
∴甲中水的质量比乙中水的质量大,
又∵水平面上物体的压力和自身的重力相等,m甲=m乙,
∴F甲>F乙;
∵两容器水的深度相同,底面积相同,
∴根据F=Ps=ρghs可知:甲、乙两容器底部受到水的压力相等.
(2)放入物块后,
V排A=(1-
| 1 |
| 3 |
| 2 |
| 3 |
| 1 |
| 4 |
| 3 |
| 4 |
∴V排A:V排B=8:9;
液体上升的高度为△h=
| V排 |
| s上 |
液体对容器底部压强的变化量为△P=ρ水g△h=ρ水g
| V排 |
| s上 |
容器底部受到水的压力变化量△F=△Ps1=ρ水g
| V排 |
| s上 |
∴甲、乙容器底部受到水的压力变化量之比为:
△F甲:△F乙=
| V排A |
| s上甲 |
| V排B |
| s上乙 |
| V排A |
| s1 |
| V排B |
| s2 |
| V排A |
| V排B |
| s2 |
| s1 |
| 8 |
| 9 |
| 1 |
| 2 |
故选D.
点评:本题考查了压力和液体压强、对容器底部压力的计算,关键是公式的灵活应用,难点是利用物体的浮沉条件和阿基米德原理求出放入物体后液体深度变化量的计算.

练习册系列答案
相关题目
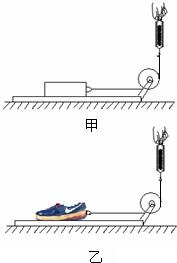 (2010?昌平区一模)水平桌面上有一个长方体橡胶块和一只橡胶底运动鞋(二者橡胶种类相同),一个一端带有定滑轮的长 木板、一些细线和一个满足实验要求的弹簧测力计.老师希望同学们用实验判断长方体橡胶块和橡胶底运动鞋的底面粗糙程度不同.小雪分别用细线系住长方体橡胶块和橡胶底运动鞋,先后在长木板上匀速拉动长方体橡胶块和橡胶底运动鞋,分别如图甲和乙所示,匀速拉动过程中分别记下弹簧测力计的示数F1和F2.她发现F2>F1,于是她得出长方体橡胶块和橡胶底运动鞋的底面粗糙程度不同.小雨指出小雪的实验方法是不正确的.请你仅利用小雪用到的实验器材,设计一个实验判断长方体橡胶块和橡胶底运动鞋的底面的粗糙程度是否一样.写出主要实验步骤和相应的实验现象与结论.
(2010?昌平区一模)水平桌面上有一个长方体橡胶块和一只橡胶底运动鞋(二者橡胶种类相同),一个一端带有定滑轮的长 木板、一些细线和一个满足实验要求的弹簧测力计.老师希望同学们用实验判断长方体橡胶块和橡胶底运动鞋的底面粗糙程度不同.小雪分别用细线系住长方体橡胶块和橡胶底运动鞋,先后在长木板上匀速拉动长方体橡胶块和橡胶底运动鞋,分别如图甲和乙所示,匀速拉动过程中分别记下弹簧测力计的示数F1和F2.她发现F2>F1,于是她得出长方体橡胶块和橡胶底运动鞋的底面粗糙程度不同.小雨指出小雪的实验方法是不正确的.请你仅利用小雪用到的实验器材,设计一个实验判断长方体橡胶块和橡胶底运动鞋的底面的粗糙程度是否一样.写出主要实验步骤和相应的实验现象与结论. (2010?昌平区一模)图是小明用滑轮组从水池中用密闭容器A提取水的装置示意图,当容器A 到达水面前,在空气中匀速下降过程中,小明对绳子竖直向下的拉力为F1,水平地面对小明的支持力为N1;当容器A完全浸没在水中(容器A未与水池底接触),且整个装置处于静止状态时,容器A在水中受到浮力为40N,小明对绳子竖直向下的拉力为为F2,水平地面对小明的支持力为N2;浸没后容器A仍能继续下沉,当容器A下沉到一定深度时,容器侧壁的阀门会自动打开,水会注入容器,注满水后,阀门自动关闭.提升注满水的容器A匀速上升的过程中(容器未露出水面),小明对绳子竖直向下的拉力为F3,水平地面对小明的支持力为N3.已知小明所受重力为500N,N1:N2=46:47,N2:N3=47:41.(不计绳重、滑轮与轴的摩擦及水的阻力,g取10N/kg)
(2010?昌平区一模)图是小明用滑轮组从水池中用密闭容器A提取水的装置示意图,当容器A 到达水面前,在空气中匀速下降过程中,小明对绳子竖直向下的拉力为F1,水平地面对小明的支持力为N1;当容器A完全浸没在水中(容器A未与水池底接触),且整个装置处于静止状态时,容器A在水中受到浮力为40N,小明对绳子竖直向下的拉力为为F2,水平地面对小明的支持力为N2;浸没后容器A仍能继续下沉,当容器A下沉到一定深度时,容器侧壁的阀门会自动打开,水会注入容器,注满水后,阀门自动关闭.提升注满水的容器A匀速上升的过程中(容器未露出水面),小明对绳子竖直向下的拉力为F3,水平地面对小明的支持力为N3.已知小明所受重力为500N,N1:N2=46:47,N2:N3=47:41.(不计绳重、滑轮与轴的摩擦及水的阻力,g取10N/kg)