题目内容
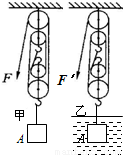
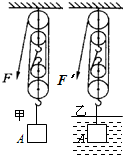 如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则:
如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则:
(1)图甲中,将正方体A匀速提起,动滑轮总重为16N,则机械效率为多大?
(2)图甲中,若正方体A在8s内上升了4m,则拉力F 的功率是多大?(写出该小题的解题思路后再求解)
(3)图乙中,若将此正方体A浸没在水中,慢慢上提(正方体未露出水面,且水的阻力不计),此时滑轮组的机械效率多大?(请在乙图中画出正方体A的受力示意图)
解:
(1)正方体的重力为G=mg=ρVg=ρa3g=8×103kg/m3×(0.1m)3×9.8N/kg=78.4N;
滑轮组的机械效率为η= =
=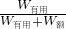 =
=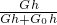 =
=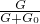 =
=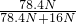 ≈83%;
≈83%;
(2)作用在绳子末端的拉力是物重和动滑轮重的 ,绳子拉下的长度是物体上升高度的4倍,拉力和绳子拉下长度之积是拉力做的功,拉力做的功与所用时间之比就是拉力的功率.
,绳子拉下的长度是物体上升高度的4倍,拉力和绳子拉下长度之积是拉力做的功,拉力做的功与所用时间之比就是拉力的功率.
作用在绳子末端的拉力为F= (G+G0)=
(G+G0)= ×(78.4N+16N)=23.6N
×(78.4N+16N)=23.6N
绳子末端拉下的长度为S=4h=4×4m=16m
拉力做的功为W=FS=23.6N×16m=377.6J
拉力的功率为P=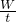 =
=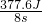 =47.2W;
=47.2W;
(3)正方体浸没时受到的浮力为F浮=ρ液gV排=1.0×103kg/m3×9.8N/kg×(0.1m)3=9.8N
滑轮组对正方体的拉力为F′=G-F浮=78.4N-9.8N=68.6N
此时滑轮组的机械效率为η′=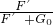 =
=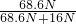 ≈81%.
≈81%.
答:
(1)滑轮组的机械效率为83%;
(2)拉力的功率为47.2W;
(3)此时滑轮组的机械效率为81%.
分析:(1)已知正方体的边长,可以得到其体积;已知正方体的密度和体积,利用公式m=ρV得到正方体的质量;已知质量,利用公式G=mg得到其重力;不计绳重和摩擦,已知物重和动滑轮重,利用公式η=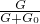 计算滑轮组机械效率.
计算滑轮组机械效率.
(2)由图知,承担物重的绳子有4股,不计绳重和摩擦,提起物体所用的拉力是物重和动滑轮重的四分之一;已知物体上升的高度和承担物重的绳子股数,可以得到绳子末端拉下的长度;已知拉力和绳子拉下的长度,利用公式W=FS得到拉力做的功;已知拉力做的功和所用时间,利用公式P=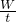 得到拉力的功率;
得到拉力的功率;
(3)已知正方体的体积和水的密度,利用公式F浮=ρ液gV排计算正方体浸没在水中受到的浮力;已知正方体受到的重力和浮力,可以得到滑轮组对正方体的拉力F′,不计绳重和摩擦,已知拉力F′和动滑轮重,利用公式η=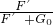 计算此时滑轮组机械效率.
计算此时滑轮组机械效率.
点评:此题给我们的启示:同一滑轮组,不仅绳重和摩擦,机械效率的大小与滑轮组施加的拉力有关,拉力越大机械效率越高.
(1)正方体的重力为G=mg=ρVg=ρa3g=8×103kg/m3×(0.1m)3×9.8N/kg=78.4N;
滑轮组的机械效率为η=
 =
=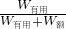 =
=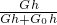 =
=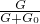 =
=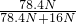 ≈83%;
≈83%;(2)作用在绳子末端的拉力是物重和动滑轮重的
 ,绳子拉下的长度是物体上升高度的4倍,拉力和绳子拉下长度之积是拉力做的功,拉力做的功与所用时间之比就是拉力的功率.
,绳子拉下的长度是物体上升高度的4倍,拉力和绳子拉下长度之积是拉力做的功,拉力做的功与所用时间之比就是拉力的功率.作用在绳子末端的拉力为F=
 (G+G0)=
(G+G0)= ×(78.4N+16N)=23.6N
×(78.4N+16N)=23.6N绳子末端拉下的长度为S=4h=4×4m=16m
拉力做的功为W=FS=23.6N×16m=377.6J
拉力的功率为P=
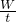 =
=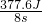 =47.2W;
=47.2W;(3)正方体浸没时受到的浮力为F浮=ρ液gV排=1.0×103kg/m3×9.8N/kg×(0.1m)3=9.8N
滑轮组对正方体的拉力为F′=G-F浮=78.4N-9.8N=68.6N
此时滑轮组的机械效率为η′=
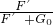 =
=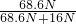 ≈81%.
≈81%.答:
(1)滑轮组的机械效率为83%;
(2)拉力的功率为47.2W;
(3)此时滑轮组的机械效率为81%.
分析:(1)已知正方体的边长,可以得到其体积;已知正方体的密度和体积,利用公式m=ρV得到正方体的质量;已知质量,利用公式G=mg得到其重力;不计绳重和摩擦,已知物重和动滑轮重,利用公式η=
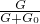 计算滑轮组机械效率.
计算滑轮组机械效率.(2)由图知,承担物重的绳子有4股,不计绳重和摩擦,提起物体所用的拉力是物重和动滑轮重的四分之一;已知物体上升的高度和承担物重的绳子股数,可以得到绳子末端拉下的长度;已知拉力和绳子拉下的长度,利用公式W=FS得到拉力做的功;已知拉力做的功和所用时间,利用公式P=
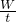 得到拉力的功率;
得到拉力的功率;(3)已知正方体的体积和水的密度,利用公式F浮=ρ液gV排计算正方体浸没在水中受到的浮力;已知正方体受到的重力和浮力,可以得到滑轮组对正方体的拉力F′,不计绳重和摩擦,已知拉力F′和动滑轮重,利用公式η=
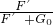 计算此时滑轮组机械效率.
计算此时滑轮组机械效率.点评:此题给我们的启示:同一滑轮组,不仅绳重和摩擦,机械效率的大小与滑轮组施加的拉力有关,拉力越大机械效率越高.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 (2012?青岛模拟)如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则:
(2012?青岛模拟)如图,正方体A的边长为0.1m,密度为8×103kg/m3.将此物体挂在如图所示的滑轮组上,不计绳重与摩擦,则: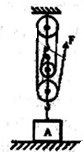 如图所示,正方体A在水平地面上处于静止状态,已知动滑轮总重为3N,作用在绳端的拉力F为5.5N,正方体A的边长为10cm,A对水平地面产生的压强为800Pa,则A物体的密度为:(忽略摩擦和绳重,绳对滑轮的拉力方向均可看成在竖直方向,g=10N/kg)( )
如图所示,正方体A在水平地面上处于静止状态,已知动滑轮总重为3N,作用在绳端的拉力F为5.5N,正方体A的边长为10cm,A对水平地面产生的压强为800Pa,则A物体的密度为:(忽略摩擦和绳重,绳对滑轮的拉力方向均可看成在竖直方向,g=10N/kg)( ) 如图所示,密度均匀的正方体A的边长为0.2米,质量为16千克.求:
如图所示,密度均匀的正方体A的边长为0.2米,质量为16千克.求: