题目内容
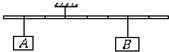 长方形水泥块长20厘米,宽10厘米,厚6厘米,密度是2×103千克/米3.把它放在水平地面上,则对地面的最大压强是
长方形水泥块长20厘米,宽10厘米,厚6厘米,密度是2×103千克/米3.把它放在水平地面上,则对地面的最大压强是分析:(1)水平面上物体对地面的压力和自身的重力相等,根据压强公式、重力公式、密度公式、体积公式得出压强的表达式,进一步根据题意得出对地面的最大压强和最小压强;
(2)均匀物体的重心在物体的几何中心上,根据图象得出它们相应的力臂,根据杠杆的平衡条件确定需在B端施加力的大小和方向.
(2)均匀物体的重心在物体的几何中心上,根据图象得出它们相应的力臂,根据杠杆的平衡条件确定需在B端施加力的大小和方向.
解答:解:(1)长方形水泥块对水平地面的压强:
P=
=
=
=
=ρgh,
所以对地面的最大压强为:
Pmax=ρghmax=2×103kg/m3×10N/kg×0.2m=4000N;
最小压强为:
Pmin=ρghmin=2×103kg/m3×10N/kg×0.06m=1200N.
(2)设杠杆长为l,杠杆平衡时,需在B端施加一个方向向上大小为F的力:
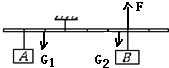
由图可知lA=
l,lB=
l,G1=
G=
×10N=3.75N,G2=G-G1=10N-3.75N=6.25N,
G1的力臂为l1=
l,G2和力F的力臂为l2=
l;
根据杠杆的平衡条件可得:
GA×lA+G1×l1=(GB-F)×lB+G2×l2,
把数据代入可得:F≈-3.96N,
即在B端施加一个方向向下大小约为3.96N的力.
故答案为:4000;1200;下;3.96.
P=
| F |
| S |
| G |
| S |
| mg |
| S |
| ρShg |
| S |
所以对地面的最大压强为:
Pmax=ρghmax=2×103kg/m3×10N/kg×0.2m=4000N;
最小压强为:
Pmin=ρghmin=2×103kg/m3×10N/kg×0.06m=1200N.
(2)设杠杆长为l,杠杆平衡时,需在B端施加一个方向向上大小为F的力:

由图可知lA=
| 2 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
| 3 |
| 8 |
G1的力臂为l1=
| 1 |
| 8 |
| 2.5 |
| 8 |
根据杠杆的平衡条件可得:
GA×lA+G1×l1=(GB-F)×lB+G2×l2,
把数据代入可得:F≈-3.96N,
即在B端施加一个方向向下大小约为3.96N的力.
故答案为:4000;1200;下;3.96.
点评:本题考查了压强和杠杆平衡条件的应用,关键是能得出均匀、规则物体对水平面压强的表达式和根据题意得出杠杆上力的大小及力臂的大小,解题过程中力的正负号表示力的方向.

练习册系列答案
 英才计划期末调研系列答案
英才计划期末调研系列答案 精英口算卡系列答案
精英口算卡系列答案
相关题目
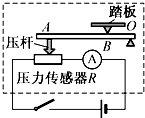 (2013?台州)有一种电子秤的原理如图,它主要由三部分构成:踏板和压力杠杆ABO,压力传感器R(电阻值会随所受压力大小发生变化的可变电阻),显示重力大小的仪表(实质是电流表).其中AO长20厘米,BO长5厘米,压力传感器R的阻值与所受压力的关系如下表所示.
(2013?台州)有一种电子秤的原理如图,它主要由三部分构成:踏板和压力杠杆ABO,压力传感器R(电阻值会随所受压力大小发生变化的可变电阻),显示重力大小的仪表(实质是电流表).其中AO长20厘米,BO长5厘米,压力传感器R的阻值与所受压力的关系如下表所示. 长方形水泥块长20厘米,宽10厘米,厚6厘米,密度是2×103千克/米3.把它放在水平地面上,则对地面的最大压强是________帕,最小压强是________帕.图中均匀木尺重10牛,A物体重30牛,B物体重20牛.为了使杠杆平衡,需在b端施加一个方向向________,大小为________牛的力.
长方形水泥块长20厘米,宽10厘米,厚6厘米,密度是2×103千克/米3.把它放在水平地面上,则对地面的最大压强是________帕,最小压强是________帕.图中均匀木尺重10牛,A物体重30牛,B物体重20牛.为了使杠杆平衡,需在b端施加一个方向向________,大小为________牛的力.