题目内容
如图甲所示,正方体A边长0.2m,作为配重使用,杠杆OE:OF=2:3,某同学用这个装置和一个密闭容器D提取水中的圆柱体B, 圆柱体B的体积是密闭容器D的 ;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的
;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的 浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的
浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的 ;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求:
;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求: (1)圆柱体B的重力;
(1)圆柱体B的重力;
(2)密闭容器D离开水面时,滑轮组提升重物B的机械效率;(百分号前面保留整数);
(3)圆柱体B的密度;
(4)在提升全过程中配重A对地面的压强的最大变化量。
(1)200N(2)83% (3)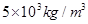 (4)
(4)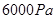
解析试题分析:由图象可知D完全露出水面时F1的功率,知道D上升的速度,求出拉力端移动的速度,利用P=Fv求拉力大小;把B放在C上,且放开手后,知道浮体C露出水面的体积减少总体积的 7/25,可得GB+F1=ρ水g 7/25VC,据此求圆柱体B的重力;对圆柱体做的功为有用功利用W=Gh计算,拉力做的功为总功利用W=Fs计算,再利用效率公式求此装置的机械效率;绳的重力,滑轮与轴的摩擦及水的阻力不计,利用F= 1/3(GB+GD+G轮)求容器D和动滑轮总重,由图可知,D未出水面时的功率,利用P=Fv求此时拉力,再根据F=1/3(GB+GD+G轮-F浮)求此时容器D受浮力大小,
再根据阿基米德原理求容器D的体积,根据圆柱体B的体积是密闭容器D的1/3求圆柱体B的体积;利用G=mg=ρvg求圆柱体B的密度;有4股绳子提定滑轮,定滑轮对杠杆右端的最大拉力Fmax=4F1+G定,由杠杆平衡条件Fmax×OF=FE1×OE求出杠杆左边的最大拉力;定滑轮对杠杆右端的最小拉力Fmin=4F2+G定,由杠杆平衡条件求出杠杆左边的最小拉力;求出杠杆左边受到的拉力变化量,利用压强公式求配重A对地面的压强的最大变化量;解:(1)由图象可知D完全露出水面时F1的功率P1=12W,P1=F1υ
解之 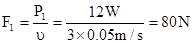
B放在C上,且放开手后, 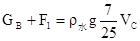
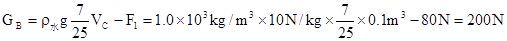
(2)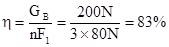
(3)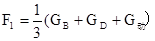
GD+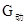 =3F1-GB=3×80N-200N=40N
=3F1-GB=3×80N-200N=40N
D未出水面时的功率为P2=6W,拉力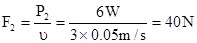
又 F2=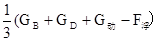
所以D受浮力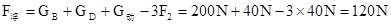
又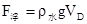 解得VD=0.012m3, VB=0.004m3
解得VD=0.012m3, VB=0.004m3
所以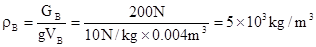
(4)定滑轮对杠杆右端的最大拉力 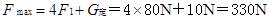
定滑轮对杠杆右端的最小拉力由杠杆平衡条件,有
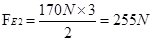
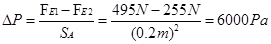
考点:滑轮(组)的机械效率、压强的大小及其计算、阿基米德原理
点评:解决本题的关键是灵活选用公式,仔细分析题图明白题意、从图象得出相关信息。



 ;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的
;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的 浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的
浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的 ;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求:(7分)
;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求:(7分)
 ;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的
;旁边浮体C的体积是0.1m3,该同学站在浮体C上,总体积的 浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的
浸入水中;该同学用力拉动滑轮组绕绳自由端,手拉绳的功率P和密闭容器D匀速被提升的距离关系如图24乙所示;密闭容器D上升速度0.05m/s保持不变,密闭容器D被提出水后,圆柱体B从密闭容器D中取出放在浮体C的上面,同时手松开绳子时,浮体C露出水面的体积减少总体积的 ;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求:
;在提升全过程中,配重A始终没有离开地面。两个定滑轮总重10 N.(绳的重力,滑轮与轴的摩擦及水的阻力不计。g=10N/kg),求: (1)圆柱体B的重力;
(1)圆柱体B的重力;