Question

【题目】一辆汽车不慎陷入泥坑，司机用图所示的滑轮组将汽车拖出．已知整个过程中，水平拉力F是1×104N，汽车沿水平方向匀速移动了4m，滑轮组的机械效率为80%．求：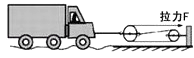

（1）拉力F做的总功．
（2）有用功为多大？

Answer 1

【答案】
（1）解：由图可知，承担车的拉力的绳子股数n=3，

则拉力端移动的距离：s=3s物=3×4m=12m，

拉力做的总功：W总=Fs=1×104N×12m=1.2×105J；

答：拉力F做的总功为1.2×105J；

（2）解：由η= =80%得对车做的有用功：

W有用=W总×η=1.2×105J×80%=9.6×104J．

答：有用功为9.6×104J．

【解析】（1）由承担车的拉力的绳子股数得出绳子自由端（拉力）移动的距离s，由W总=Fs计算拉力做的总功；

（2）知道滑轮组的机械效率，由机械效率的公式计算对车做的有用功（克服阻力做的功）．

【考点精析】根据题目的已知条件，利用机械效率和滑轮（组）的机械效率的相关知识可以得到问题的答案，需要掌握机械效率：有用功跟总功的比值，用η表示．即：η= W有用 / W总 机械效率一般用百分数表示．有用功是总功的一部分，且额外功总是客观存在的，则有W有用 < W总 ，因此η总是小于1 ，这也表明：使用任何机械都不能省功；关于滑轮组机械效率的计算：W有用 = G·h；W总 = F·s； s = n·h （1）η=W有用 / W总 （2)η= W有用 / W总 = Gh/Fs = Gh/nFh = G/(nF)．