Question

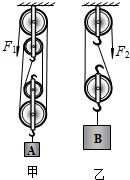（2012?桂平市三模）如图所示，A、B重G_A：G_B=1：3，用甲、乙两滑轮组分别匀速提升A、B两物体，在相同时间内两物体被提升高度分别为h_A和h_B，2h_A=5h_B．已知两滑轮组动滑轮重分别为G_甲和G_乙，且G_甲：G_乙=1：3．两滑轮组的机械效率分别为η₁和η₂，功率分别为P₁和P₂．若不计绳重和滑轮轴处摩擦，则下列判断正确的是（　　）

A．η₁：η₂=1：1

B．F₁：F₂=3：8

C．P₁：P₂=5：3

D．v_A：v_B=2：5

Answer 1

分析：知道两图提升物体重的大小关系和动滑轮重的大小关系，利用F=

1

n

（G_物+G_轮）求拉力的大小关系；
又知道提升高度的关系，利用s=nh求拉力端移动距离的大小关系，利用效率公式求两图效率之比；
求出了拉力之比、拉力移动距离之比，利用W=Fs求拉力做功之比，因为是在相同的时间内，可求拉力做功功率之比；
知道在相同时间内两物体被提升高度关系，利用速度公式可得两物体移动速度的大小关系．

解答：解：由题知，G_A：G_B=1：3，G_甲：G_乙=1：3．
设G_A=G，G_甲=G′，则G_B=3G，G_乙=3G′，
∵不计绳重和滑轮轴处摩擦，
∴F₁=

1

4

（G_A+G_甲）=

1

4

（G+G′），
F₂=

1

2

（G_B+G_乙）=

1

2

（3G+3G′），
∴F₁：F₂=

1

4

（G+G′）：

1

2

（3G+3G′）=1：6，故B错；
η₁=

GA hA

F1sA

=

GAhA

F14hA

=

G

4×F1

，
η₂=

GBhB

F2sB

=

3G hB

F22hB

=

3G

2×F2

，
∴η₁：η₂=

G

4×F1

：

3G

2×F2

=

G

4×F1

×

2×F2

3G

=

G

3G

×

2×F2

4×F1

=

1

3

×

2×6

4×1

=1：1，故A正确；
拉力移动距离之比：
s_A：s_B=4h_A：2h_B=

4hA

2hB

=

4×5

2×2

=5：1，
拉力做功之比：
W₁：W₂=F₁s_A：F₂s_B=

F1sA

F2sB

=

1×5

6×1

=5：6；
∵做功时间相同，
∴功率之比：
P₁：P₂=W₁：W₂=5：6，故C错；
两物体移动速度之比：
v_A：v_B=

hA

t

：

hB

t

=h_A：h_B=5：2，故D错．
故选A．

点评：本题考查了速度的计算、功率的计算、使用滑轮组拉力的计算、机械效率的计算，根据题图确定n的大小（直接从动滑轮上引出的绳子股数）是本题的突破口，利用好不计绳重和摩擦时拉力和物重的关系[F=

1

n

（G_轮+G_物）]是本题的关键．