题目内容
如图所示装置,水深为2米.一边长为0.2米的正方体物块完全浸没在水中并沉入水底时,整个装置处于平衡状态,AO=2OB,物块重G=100N,当小明用力F拉动绳子使物块上升1米时,求:(g=10N/kg ρ水=1.0×103kg/m3)①物块受到的水的浮力为多少牛顿?
②物块在水中上升的过程中小明拉动绳子的力F拉为多少牛顿?
③如果拉力F=10N,拉力F所做的功为多少焦耳?
④此装置的机械效率为多少?
⑤当物体沉入水底时物块上表面所受水的压力为多少牛顿?
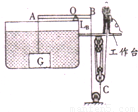
【答案】分析:(1)知道正方体物块的边长,求出物块的体积(排开水的体积),利用阿基米德原理求物块受到的水的浮力;
(2)物块在水中上升的过程中,受到重力等于拉力加上浮力,据此求出A端受到的拉力,知道两力臂大小关系,根据杠杆平衡条件B端拉力大小;而滑轮组n=5,则可求小明的拉力;
(3)知道拉力大小,由图知,知道物块上升高度h,B端下降hB= h,而拉力端移动的距离s=5hB,利用W=Fs求拉力F所做的功(总功);
h,而拉力端移动的距离s=5hB,利用W=Fs求拉力F所做的功(总功);
(4)利用该装置做的有用功是杠杆A端对物体拉力做的功,再利用效率公式求此装置的机械效率;
(5)求出当物体沉入水底时物块上表面所处的深度,利用液体压强公式求上表面受到水的压强,利用F=pS求上表面受水的压力.
解答:解:
(1)∵正方体物块完全浸没在水中,
∴物块排开水的体积:
V排=V=(0.2m)3=0.008m3,
物块受到的水的浮力:
F浮=ρ水V排g=1×103kg/m3×10N/kg×0.008m3=80N;
(2)∵FA+F浮=G
∴FA=G-F浮=100N-80N=20N;
∵FA×OA=FB×OB,
即:20N×2OB=FB×OB,
∴FB=40N,
∵n=5,
∴F拉= FB=
FB= ×40N=8N;
×40N=8N;
(3)物块上升h,B端下降hB= h=0.5m,
h=0.5m,
拉力端移动的距离:
s=5hB=5×0.5m=2.5m,
拉力F所做的功(总功):
W=Fs=10N×2.5m=25J;
(4)W有用=FAh=20N×1m=20J,
此装置的机械效率:
η= =
=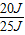 =80%;
=80%;
(5)当物体沉入水底时物块上表面所处的深度:
h=2m-0.2m=1.8m,
上表面受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×0.18m=1800N,
上表面受水的压力:
F=pS=1800N×0.2m×0.2m=72N.
答:①物块受到的水的浮力为80N;
②物块在水中上升的过程中小明拉动绳子的力F拉为8N;
③如果拉力F=10N,拉力F所做的功为25J;
④此装置的机械效率为80%;
⑤当物体沉入水底时物块上表面所受水的压力为72N.
点评:本题考查了学生对阿基米德原理、杠杆平衡条件、滑轮组机械效率公式、液体压强公式的理解和掌握,关键是公式的灵活运用,易错点:使用此装置有用功和额外功的确定、拉力端移动距离的计算.
(2)物块在水中上升的过程中,受到重力等于拉力加上浮力,据此求出A端受到的拉力,知道两力臂大小关系,根据杠杆平衡条件B端拉力大小;而滑轮组n=5,则可求小明的拉力;
(3)知道拉力大小,由图知,知道物块上升高度h,B端下降hB=
 h,而拉力端移动的距离s=5hB,利用W=Fs求拉力F所做的功(总功);
h,而拉力端移动的距离s=5hB,利用W=Fs求拉力F所做的功(总功);(4)利用该装置做的有用功是杠杆A端对物体拉力做的功,再利用效率公式求此装置的机械效率;
(5)求出当物体沉入水底时物块上表面所处的深度,利用液体压强公式求上表面受到水的压强,利用F=pS求上表面受水的压力.
解答:解:
(1)∵正方体物块完全浸没在水中,
∴物块排开水的体积:
V排=V=(0.2m)3=0.008m3,
物块受到的水的浮力:
F浮=ρ水V排g=1×103kg/m3×10N/kg×0.008m3=80N;
(2)∵FA+F浮=G
∴FA=G-F浮=100N-80N=20N;
∵FA×OA=FB×OB,
即:20N×2OB=FB×OB,
∴FB=40N,
∵n=5,
∴F拉=
 FB=
FB= ×40N=8N;
×40N=8N;(3)物块上升h,B端下降hB=
 h=0.5m,
h=0.5m,拉力端移动的距离:
s=5hB=5×0.5m=2.5m,
拉力F所做的功(总功):
W=Fs=10N×2.5m=25J;
(4)W有用=FAh=20N×1m=20J,
此装置的机械效率:
η=
 =
=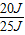 =80%;
=80%;(5)当物体沉入水底时物块上表面所处的深度:
h=2m-0.2m=1.8m,
上表面受到水的压强:
p=ρgh=1×103kg/m3×10N/kg×0.18m=1800N,
上表面受水的压力:
F=pS=1800N×0.2m×0.2m=72N.
答:①物块受到的水的浮力为80N;
②物块在水中上升的过程中小明拉动绳子的力F拉为8N;
③如果拉力F=10N,拉力F所做的功为25J;
④此装置的机械效率为80%;
⑤当物体沉入水底时物块上表面所受水的压力为72N.
点评:本题考查了学生对阿基米德原理、杠杆平衡条件、滑轮组机械效率公式、液体压强公式的理解和掌握,关键是公式的灵活运用,易错点:使用此装置有用功和额外功的确定、拉力端移动距离的计算.

练习册系列答案
相关题目
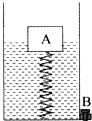 在探究浮沉条件时设计了如图所示装置,在容器底部固定一轻质弹簧,上方连有长方体木块A,容器底部有一个出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好没有发生形变.(不计弹簧受到的浮力,g取10N/kg)
在探究浮沉条件时设计了如图所示装置,在容器底部固定一轻质弹簧,上方连有长方体木块A,容器底部有一个出水口,当容器中水深为20cm时,木块A有2/5的体积浸在水中,此时弹簧恰好没有发生形变.(不计弹簧受到的浮力,g取10N/kg)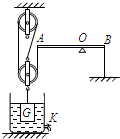 (2011?怀柔区二模)如图所示装置中,杠杆和滑轮的重力及滑轮的摩擦均可忽略不计,杠杆AB可以绕O点在竖直平面内自由转动,A端通过竖直方向的轻绳与滑轮组相连,在B端用一轻绳沿竖直方向将杠杆拉住,使其始终保持水平平衡.在滑轮组的下方,悬挂一圆柱形的物体,此物体被浸在圆柱形容器内的液体中.已知杠杆O点两侧的长度关系为AO=2OB,圆柱形物体的底面积为10cm2、高为12cm,圆柱形容器的底面积为50cm2.若容器中的液体为水,在水深为20cm时物体的上表面恰与水面相平,此时杠杆B端绳上的拉力为F1;打开圆柱形容器下方的阀门K,将水向外释放,直到物体露出水面的体积为其总体积的2/3时,将阀门K关闭,此时杠杆B端绳上的拉力为F2,且F1:F2=3:5.若容器中液体为某种未知液体,其质量与最初容器中的水的质量相等,此时未知液体的深度为18cm,杠杆B端绳上的拉力为F3.(取g=10N/kg)
(2011?怀柔区二模)如图所示装置中,杠杆和滑轮的重力及滑轮的摩擦均可忽略不计,杠杆AB可以绕O点在竖直平面内自由转动,A端通过竖直方向的轻绳与滑轮组相连,在B端用一轻绳沿竖直方向将杠杆拉住,使其始终保持水平平衡.在滑轮组的下方,悬挂一圆柱形的物体,此物体被浸在圆柱形容器内的液体中.已知杠杆O点两侧的长度关系为AO=2OB,圆柱形物体的底面积为10cm2、高为12cm,圆柱形容器的底面积为50cm2.若容器中的液体为水,在水深为20cm时物体的上表面恰与水面相平,此时杠杆B端绳上的拉力为F1;打开圆柱形容器下方的阀门K,将水向外释放,直到物体露出水面的体积为其总体积的2/3时,将阀门K关闭,此时杠杆B端绳上的拉力为F2,且F1:F2=3:5.若容器中液体为某种未知液体,其质量与最初容器中的水的质量相等,此时未知液体的深度为18cm,杠杆B端绳上的拉力为F3.(取g=10N/kg) 如图所示装置,水深为2米.一边长为0.2米的正方体物块完全浸没在水中并沉入水底时,整个装置处于平衡状态,AO=2OB,物块重G=100N,当小明用力F拉动绳子使物块上升1米时,求:(g=10N/kg ρ水=1.0×103kg/m3)
如图所示装置,水深为2米.一边长为0.2米的正方体物块完全浸没在水中并沉入水底时,整个装置处于平衡状态,AO=2OB,物块重G=100N,当小明用力F拉动绳子使物块上升1米时,求:(g=10N/kg ρ水=1.0×103kg/m3) 如图所示装置,水深为2米.一边长为0.2米的正方体物块完全浸没在水中并沉入水底时,整个装置处于平衡状态,AO=2OB,物块重G=100N,当小明用力F拉动绳子使物块上升1米时,求:(g=10N/kg ρ水=1.0×103kg/m3)
如图所示装置,水深为2米.一边长为0.2米的正方体物块完全浸没在水中并沉入水底时,整个装置处于平衡状态,AO=2OB,物块重G=100N,当小明用力F拉动绳子使物块上升1米时,求:(g=10N/kg ρ水=1.0×103kg/m3)