题目内容
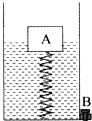在探究浮沉条件时设计了如图所示装置，在容器底部固定一轻质弹簧，上方连有长方体木块A，容器底部有一个出水口，当容器中水深为20cm时，木块A有2/5的体积浸在水中，此时弹簧恰好没有发生形变．（不计弹簧受到的浮力，g取10N/kg）（1）该木块A的密度为
0.4×103
0.4×103
kg/m3．此时容器底受到水的压强为2×103
2×103
Pa．（2）向容器内缓慢加水，直至木块A刚好完全浸没水中，立即停止加水，此时弹簧对木块A 的作用力为F1，在原图上画出此时水面的大致位置．
（3）打开阀门B缓慢放水，直至木块A刚好完全离开水面时，立即关闭阀门B，此时弹簧对木块A的作用力为F2，则F1、F2之比是
3：2
3：2
．分析：（1）弹簧没有发生形变，说明木块A只受两个力的作用：重力和浮力，且两者为一对平衡力；根据物体漂浮时，排开液体体积与密度成反比得到木块的密度．
已知容器中水的深度，利用P=ρgh可以计算水对容器底的压强．
（2）弹簧对木块有向下的拉力，所以向容器中加水时，随着木块浸入水中体积的增大，所受浮力增大，直到木块完全浸没浮力不再变化．
（3）木块完全浸没时，弹簧对木块有向下的拉力F1；木块离开水面时，弹簧对木块有向上的支持力F2，分别计算F1、F2的大小，就能得到两者之比．
已知容器中水的深度，利用P=ρgh可以计算水对容器底的压强．
（2）弹簧对木块有向下的拉力，所以向容器中加水时，随着木块浸入水中体积的增大，所受浮力增大，直到木块完全浸没浮力不再变化．
（3）木块完全浸没时，弹簧对木块有向下的拉力F1；木块离开水面时，弹簧对木块有向上的支持力F2，分别计算F1、F2的大小，就能得到两者之比．
解答：解：
（1）木块漂浮时
=
=
所以木块的密度为ρ木=
ρ水=0.4×103kg/m3；
水对容器底的压强为P=ρgh=1.0×103kg/m3×10N/kg×0.2m=2×103Pa
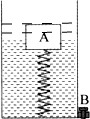
（2）木块完全浸没时，受到的浮力最大，此时弹簧略向上伸长，所以画水面位置时，应在木块位置略高一些．
（3）木块完全浸没时，弹簧对木块的作用力F1=F浮-G=ρ水gV-ρ木gV=0.6ρ水gV
木块离开水面后，弹簧对木块的作用力F2=G=ρ木gV=0.4ρ水gV
=
=
故答案为：
（1）0.4×103；2×103
（2）木块浸没后水面所在位置如下图
（3）3：2
（1）木块漂浮时
| ρ木 |
| ρ水 |
| V排 |
| V |
| 2 |
| 5 |
所以木块的密度为ρ木=
| 2 |
| 5 |
水对容器底的压强为P=ρgh=1.0×103kg/m3×10N/kg×0.2m=2×103Pa
（2）木块完全浸没时，受到的浮力最大，此时弹簧略向上伸长，所以画水面位置时，应在木块位置略高一些．
（3）木块完全浸没时，弹簧对木块的作用力F1=F浮-G=ρ水gV-ρ木gV=0.6ρ水gV
木块离开水面后，弹簧对木块的作用力F2=G=ρ木gV=0.4ρ水gV
| F1 |
| F2 |
| 0.6ρ水gV |
| 0.4ρ水gV |
| 3 |
| 2 |
故答案为：
（1）0.4×103；2×103
（2）木块浸没后水面所在位置如下图
（3）3：2
点评：在此题中弹簧对木块的作用力方向不同：木块浸没时，弹簧对木块有向下的拉力，木块离开水后，弹簧对木块有向上的支持力，明确这一点是正确解答的关键．
练习册系列答案
新思维寒假作业系列答案
相关题目
在“探究物体的浮沉条件”时，小敏同学从家中带来了一些物品，其中有①小铁钉、②软木塞、③蜡烛、④苹果、⑤塑料块、⑥小石块．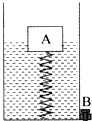
在探究浮沉条件时设计了如图所示装置，在容器底部固定一轻质弹簧，上方连有长方体木块A，容器底部有一个出水口，当容器中水深为20cm时，木块A有2/5的体积浸在水中，此时弹簧恰好没有发生形变．（不计弹簧受到的浮力，g取10N/kg）
