题目内容
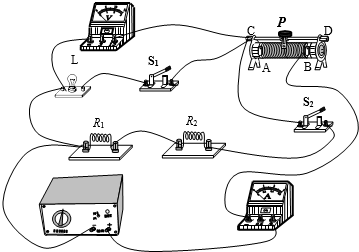
如图所示电路,小灯泡标有“6V 0.3A”,R1是定值电阻,R2是滑动变阻器,电源电压保持不变。当开关S闭合,滑动变阻器滑片P位于a点时,小灯泡正常发光,其电功率为PL,电压表V2的示数为Ua,R1与R2的电功率分别为P1a、Pa,电路的总电功率为P总;当滑动变阻器的滑片P移动到b点时,小灯泡的电功率为PL/,电压表V2的示数为Ub,R1与R2的电功率分别为P1b、Pb,电路的总电功率为P总/。若P总∶P总/=3∶2,PL∶PL/=9∶2,P1a-P1b=0.75W,Pb-Pa=0.95W。

求:⑴小灯泡正常发光时灯丝的电阻和定值电阻R1的阻值
⑵电压表V1的示数
⑶电压表V2的示数Ua和Ub。(6分)
⑴20Ω,15Ω⑵1.5V,7V
解析:解:当开关S闭合后,小灯泡与R1和R2串联,滑动变阻器滑片P分别位于a、b两点时的等效电路图分别如图1、2所示。
|
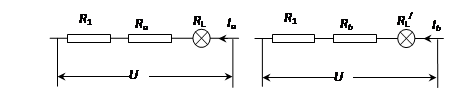

当滑动变阻器的滑片位于a点时,小灯泡正常发光,Ia =0.3A, RL=U/Ia=6V/0.3A=20Ω
由电源电压不变 P总∶P总/=U·Ia∶U·Ib = Ia∶Ib =3∶2
Ib =2×0.3A/3=0.2A
R1 为定值电阻,由P =I2·R得到P1a-P1b= Ia2·R1-Ib2·R1 =(0.3A)2 R1-(0.2A)2 R1=0.75W
R1=15Ω ………………………………1分
由P =I2·R, PL∶PL/= Ia2·RL-Ib2·RL/=(0.3A)2 ×20Ω-(0.2A)2 RL/=9∶2
RL/=10Ω
由电源电压不变和欧姆定律U=I·R,R总=RL+R1+Ra,R总/= RL/+R1+Rb
Ia·R总= Ib·R总/ 0.3A(20Ω+15Ω+Ra)=0.2A(10Ω+15Ω+Rb)
即2Rb-3 Ra=55 ①
Pb-Pa= Ia2·Ra-Ib2·Rb= (0.2A)2×Rb -(0.3A)2×Ra =0.95W
即4 Rb-9Ra =95 ②
由①②式解出:Rb=35Ω Ra=5Ω
Ua=Ia·Ra=0.3A×5Ω=1.5V …………………………1分
Ub=Ib·Rb=0.2A×35Ω=7V …………………………1分
电压表V1测的是电源电压
U=I·R =Ia·R总=0.3A×(20Ω+15Ω+5Ω) =12V …………………………1分
当开关S闭合后,小灯泡与R1和R2串联,当滑动变阻器的滑片位于a点时,小灯泡正常发光,Ia =0.3A,RL=U/Ia=6V/0.3A=20Ω
由电源电压不变 P总∶P总/=U·Ia∶U·Ib = Ia∶Ib =3∶2
Ib =2×0.3A/3=0.2A
R1 为定值电阻,由P =I2·R得到P1a-P1b= Ia2·R1-Ib2·R1 =(0.3A)2 R1-(0.2A)2 R1=0.75W
R1=15Ω
由P =I2·R, PL∶PL/= Ia2·RL-Ib2·RL/=(0.3A)2 ×20Ω-(0.2A)2 RL/=9∶2
RL/=10Ω
由电源电压不变和欧姆定律U=I·R,R总=RL+R1+Ra,R总/= RL/+R1+Rb
Ia·R总= Ib·R总/ 0.3A(20Ω+15Ω+Ra)=0.2A(10Ω+15Ω+Rb)
即2Rb-3 Ra=55 ①
Pb-Pa= Ia2·Ra-Ib2·Rb= (0.2A)2×Rb -(0.3A)2×Ra =0.95W
即4 Rb-9Ra =95 ②
由①②式解出:Rb=35Ω Ra=5Ω
Ua=Ia·Ra=0.3A×5Ω=1.5V
Ub=Ib·Rb=0.2A×35Ω=7V
电压表V1测的是电源电压
U=I·R =Ia·R总=0.3A×(20Ω+15Ω+5Ω) =12V

 阅读快车系列答案
阅读快车系列答案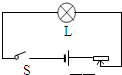 如图所示电路,小灯泡标有“6V 6W”字样,滑动变阻器标有“12Ω 2A”.闭合开关,滑动变阻器的滑片滑到最左端时,小灯泡正常发光.(设灯丝的电阻不变)滑动变阻器的滑片移动过程中以下说法正确的是( )
如图所示电路,小灯泡标有“6V 6W”字样,滑动变阻器标有“12Ω 2A”.闭合开关,滑动变阻器的滑片滑到最左端时,小灯泡正常发光.(设灯丝的电阻不变)滑动变阻器的滑片移动过程中以下说法正确的是( )| A、灯泡的实际功率最小值是2W | B、电源电压为12V | C、小灯泡两端的电压变化范围是2V~6V | D、灯丝电阻为8Ω |
 (2007?岳阳)小红同学用如图所示电路测小灯泡的电阻,记录数据如下表
(2007?岳阳)小红同学用如图所示电路测小灯泡的电阻,记录数据如下表
 (2013?道外区二模)某中学实践小组同学按如图所示电路探究小灯泡的工作情况.其中电源电压保持不变,灯L上标有“18V 18W”的字样,电压表所选量程为0~15V,电流表所选量程为0~3A.情况一:开关S闭合,滑动变阻器的滑片P移到a端时,灯L正常发光,电流表示数为2.5A;情况二:开关S断开,滑动变阻器的滑片P移到距a端四分之三ab长度时,电压表指针满偏.请回答以下问题:
(2013?道外区二模)某中学实践小组同学按如图所示电路探究小灯泡的工作情况.其中电源电压保持不变,灯L上标有“18V 18W”的字样,电压表所选量程为0~15V,电流表所选量程为0~3A.情况一:开关S闭合,滑动变阻器的滑片P移到a端时,灯L正常发光,电流表示数为2.5A;情况二:开关S断开,滑动变阻器的滑片P移到距a端四分之三ab长度时,电压表指针满偏.请回答以下问题: 某同学在用如图所示电路测小灯泡电阻的实验中,发现闭合开关以后,灯泡不亮,电流表没有示数,怎么移动滑动变阻器滑片位置,电压表的示数都不变,且均为电源电压.可能出现的问题是( )
某同学在用如图所示电路测小灯泡电阻的实验中,发现闭合开关以后,灯泡不亮,电流表没有示数,怎么移动滑动变阻器滑片位置,电压表的示数都不变,且均为电源电压.可能出现的问题是( )