题目内容
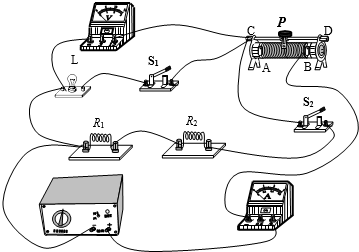
如图所示电路,小灯泡L标有“6V 3W”字样,电阻R1+R2=6Ω.当开关S1闭合、S2断开,滑动变阻器的滑片P滑到M点时,电流表的示数为I1,电压表的示数为U1,滑动变阻器的功率为PM;此时灯L正常发光.当开关S1断开、S2闭合,滑动变阻器的滑片P滑到N点时,电流表的示数为I2,电压表的示数为U2,滑动变阻器的功率为PN;已知I1:I2=3:1,PM:PN=1:1,灯电阻RL与电阻R1之比为RL:R1=3:1(假设灯丝电阻不随温度变化).求:
(1)电路两次电压表示数之比;
(2)滑动变阻器两次连入电路的阻值各多大;
(3)电源电压多大.

(1)电路两次电压表示数之比;
(2)滑动变阻器两次连入电路的阻值各多大;
(3)电源电压多大.
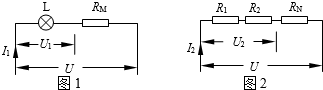
分析:先画出两种情况下的简化电路图:
(1)根据P=
求出灯泡的电阻,根据欧姆定律表示出电路两次电压表示数之比,把电流之比和阻值代入即可得出答案;
(2)根据串联电路的特点和欧姆定律表示出电源的电压,利用电源的电压不变得出等式即可求出RM、RN的阻值关系,根据P=I2R表示出滑动变阻器消耗的电功率之间的关系结合电流关系求出RM、RN的阻值关系,联立等式即可求出RM、RN的大小;
(3)根据P=UI求出图1中灯泡正常发光时电路中的电流,根据电阻的串联和欧姆定律求出电源的电压.
(1)根据P=
| U2 |
| R |
求出灯泡的电阻,根据欧姆定律表示出电路两次电压表示数之比,把电流之比和阻值代入即可得出答案;
(2)根据串联电路的特点和欧姆定律表示出电源的电压,利用电源的电压不变得出等式即可求出RM、RN的阻值关系,根据P=I2R表示出滑动变阻器消耗的电功率之间的关系结合电流关系求出RM、RN的阻值关系,联立等式即可求出RM、RN的大小;
(3)根据P=UI求出图1中灯泡正常发光时电路中的电流,根据电阻的串联和欧姆定律求出电源的电压.
解答:解:当S1闭合,S2断开时,等效电路图如图1;当S2闭合,S1断开时,等效电路图如图2;
(1)根据P=
可得,灯泡的电阻:
RL=
=
=12Ω,
根据欧姆定律可得,电路两次电压表示数之比:
=
=
×
=
×
=
;
(2)∵电源的电压不变,
∴
=
=
=
,
整理可得:RN=30Ω+3RM--------①
∵P=I2R,且PM:PN=1:1,
=
=(
)2×
=(
)2×
=
,
整理可得:RN=9RM------------②
由①②可得,RM=5Ω,RN=45Ω;
(3)图1中灯泡正常发光,则:
I1=
=
=0.5A,
则电源的电压:
U=I1(RL+RM)=0.5A×(12Ω+5Ω)=8.5V.
答:(1)电路两次电压表示数之比为6:1;
(2)滑动变阻器两次连入电路的阻值分别为5Ω、45Ω;
(3)电源电压为8.5V.

(1)根据P=
| U2 |
| R |
可得,灯泡的电阻:
RL=
| UL额2 |
| PL额 |
| (6V)2 |
| 3W |
根据欧姆定律可得,电路两次电压表示数之比:
| U1 |
| U2 |
| I1RL |
| I2(R1+R2) |
| I1 |
| I2 |
| RL |
| R1+R2 |
| 3 |
| 1 |
| 12Ω |
| 6Ω |
| 6 |
| 1 |
(2)∵电源的电压不变,
∴
| I1 |
| I2 |
| R1+R2+RN |
| RL+RM |
| 6Ω+RN |
| 12Ω+RM |
| 3 |
| 1 |
整理可得:RN=30Ω+3RM--------①
∵P=I2R,且PM:PN=1:1,
| PM |
| PN |
| I12RM |
| I22RN |
| I1 |
| I2 |
| RM |
| RN |
| 3 |
| 1 |
| RM |
| RN |
| 1 |
| 1 |
整理可得:RN=9RM------------②
由①②可得,RM=5Ω,RN=45Ω;
(3)图1中灯泡正常发光,则:
I1=
| PL |
| UL |
| 3W |
| 6V |
则电源的电压:
U=I1(RL+RM)=0.5A×(12Ω+5Ω)=8.5V.
答:(1)电路两次电压表示数之比为6:1;
(2)滑动变阻器两次连入电路的阻值分别为5Ω、45Ω;
(3)电源电压为8.5V.
点评:本题考查了串联电路的特点和欧姆定律、电功率公式的灵活应用,画出电路的简图和利用好电源的电压不变是关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
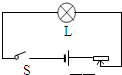 如图所示电路,小灯泡标有“6V 6W”字样,滑动变阻器标有“12Ω 2A”.闭合开关,滑动变阻器的滑片滑到最左端时,小灯泡正常发光.(设灯丝的电阻不变)滑动变阻器的滑片移动过程中以下说法正确的是( )
如图所示电路,小灯泡标有“6V 6W”字样,滑动变阻器标有“12Ω 2A”.闭合开关,滑动变阻器的滑片滑到最左端时,小灯泡正常发光.(设灯丝的电阻不变)滑动变阻器的滑片移动过程中以下说法正确的是( )| A、灯泡的实际功率最小值是2W | B、电源电压为12V | C、小灯泡两端的电压变化范围是2V~6V | D、灯丝电阻为8Ω |
 (2007?岳阳)小红同学用如图所示电路测小灯泡的电阻,记录数据如下表
(2007?岳阳)小红同学用如图所示电路测小灯泡的电阻,记录数据如下表
 (2013?道外区二模)某中学实践小组同学按如图所示电路探究小灯泡的工作情况.其中电源电压保持不变,灯L上标有“18V 18W”的字样,电压表所选量程为0~15V,电流表所选量程为0~3A.情况一:开关S闭合,滑动变阻器的滑片P移到a端时,灯L正常发光,电流表示数为2.5A;情况二:开关S断开,滑动变阻器的滑片P移到距a端四分之三ab长度时,电压表指针满偏.请回答以下问题:
(2013?道外区二模)某中学实践小组同学按如图所示电路探究小灯泡的工作情况.其中电源电压保持不变,灯L上标有“18V 18W”的字样,电压表所选量程为0~15V,电流表所选量程为0~3A.情况一:开关S闭合,滑动变阻器的滑片P移到a端时,灯L正常发光,电流表示数为2.5A;情况二:开关S断开,滑动变阻器的滑片P移到距a端四分之三ab长度时,电压表指针满偏.请回答以下问题: 某同学在用如图所示电路测小灯泡电阻的实验中,发现闭合开关以后,灯泡不亮,电流表没有示数,怎么移动滑动变阻器滑片位置,电压表的示数都不变,且均为电源电压.可能出现的问题是( )
某同学在用如图所示电路测小灯泡电阻的实验中,发现闭合开关以后,灯泡不亮,电流表没有示数,怎么移动滑动变阻器滑片位置,电压表的示数都不变,且均为电源电压.可能出现的问题是( )