题目内容
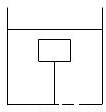
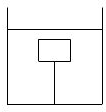如图，一块由均匀材料制成的正方体实心物块，边长为a，密度为ρ，用一根细线将物块底面的中心与容器底面中央相连，往容器中注入某种液体，使物块浸没在液体中，已知当物块静止时细线对物块竖直向下拉力的大小为F，求：物块的质量m=________，物块受到的浮力F浮=________，若剪断细线后，物块重新达到平衡状态时，其露出液面的体积V=________．
ρa3 ρga3+F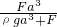 
分析：由密度公式可求得物块的质量；通过对物体受力分析，由力的合成可求出浮力；由浮力公式可表示出液体的密度，由物体的浮沉条件可求得浸入液体的体积，由浸入液体中的体积可求出露出液面的体积．
解答：已知物体的边长，则其体积V=a3，则由密度公式可得：m=ρV=ρa3
物体受重力、浮力及绳子的拉力而处于静止状态，F浮=F+mg=F+ρga3；
F浮=ρ′ga3，则ρ′=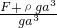
剪断细线后，由于浮力大于重力故物体上浮，当所受浮力等于重力时，物体重新平衡：
ρ′gV'=ρga3
则V'=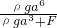
露出水面的体积为V=a3-V'=a3-=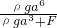
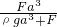
故答案为：ρa3，ρga3+F，．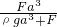
点评：本题审题是关键，应明确题中液体密度未知，应先用已知条件将其表示出来才能求露出液面的体积．
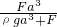
分析：由密度公式可求得物块的质量；通过对物体受力分析，由力的合成可求出浮力；由浮力公式可表示出液体的密度，由物体的浮沉条件可求得浸入液体的体积，由浸入液体中的体积可求出露出液面的体积．
解答：已知物体的边长，则其体积V=a3，则由密度公式可得：m=ρV=ρa3
物体受重力、浮力及绳子的拉力而处于静止状态，F浮=F+mg=F+ρga3；
F浮=ρ′ga3，则ρ′=
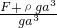
剪断细线后，由于浮力大于重力故物体上浮，当所受浮力等于重力时，物体重新平衡：
ρ′gV'=ρga3
则V'=
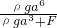
露出水面的体积为V=a3-V'=a3-
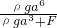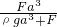
=故答案为：ρa3，ρga3+F，
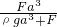．点评：本题审题是关键，应明确题中液体密度未知，应先用已知条件将其表示出来才能求露出液面的体积．
练习册系列答案
相关题目
（2000?苏州）如图所示，一块由均匀材料制成的正方体实心物块，边长为a，密度为ρ，用一根细线将物块底面的中心与容器底面中央相连．往容器内注入某种液体，使物块浸没在液体中，已知当物块静止时细线对物块竖直向下拉力的大小为F．求：
