题目内容
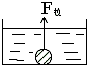 如图所示,底面积为80cm2的容器中盛有深30cm的水.将一质量为540g的实心铝球投入水中.问:
如图所示,底面积为80cm2的容器中盛有深30cm的水.将一质量为540g的实心铝球投入水中.问:
(1)铝球浸没在水中时受到的浮力是多大?
(2)投入铝球后,水对容器底部的压强增加了多少?
(3)若用一根最多能承受4N拉力的细绳系住铝球缓慢向上拉,当铝球露出水面的体积为多大时绳子会拉断?(已知ρ铝=2.7×103kg/m3,取g=10N/kg).
解:(1)根据ρ= 可得:
可得:
铝球的体积V铝=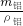 =
=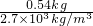 =2×10-4m3,
=2×10-4m3,
根据阿基米德原理可得:
铝球浸没在水中时受到的浮力F浮=ρ水gV排=ρ水gV铝=1×103kg/m3×10N/kg×2×10-4m3=2N;
(2)设投入铝球后水面上升的高度为△H,则:
△H= =
= =
= =0.025m,
=0.025m,
水对容器底部增加的压强:
p=ρ水g△H=1×103kg/m3×10N/kg×0.025m=250Pa;
(3)设当铝球露出水面的体积为V露时,绳子会断,此时的浮力为F浮′,
则:F浮′=G-F拉,即ρ水gV排′=G-F拉
V排′= =
= =
= =1.4×10-4m3,
=1.4×10-4m3,
铝球露出水面的体积:
V露=V-V排′=2×10-4m3-1.4×10-4m3=6×10-5m3.
答:(1)铝球浸没在水中时受到的浮力是2N;
(2)投入铝球后,水对容器底部的压强增加250Pa;
(3)若用一根最多能承受4N拉力的细绳系住铝球缓慢向上拉,当铝球露出水面的体积为1.4×10-4m3时绳子会拉断.
分析:(1)先根据V=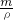 求铝球的体积,铝球浸没在水中时排开水的体积和本身的体积相等,再根据F浮=ρgV排求出铝球浸没在水中受到的浮力;
求铝球的体积,铝球浸没在水中时排开水的体积和本身的体积相等,再根据F浮=ρgV排求出铝球浸没在水中受到的浮力;
(2)根据V=Sh求出铝球浸没时容器内水上升的高度,再根据p=ρgh求出容器底部压强的增加量;
(3)根据G=mg可知铝球的重力,绳恰好断掉时绳的拉力为4N,此时水中的铝块受到得浮力等于铝块重减去绳子的拉力,根据阿基米德原理可计算铝块在水中的体积,铝块露出水面的体积V露=V-V排.
点评:本题是一道力学综合题,要求灵活运用密度公式、重力公式、液体压强公式、阿基米德原理和力的合成,难度较大.
 可得:
可得:铝球的体积V铝=
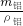 =
=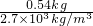 =2×10-4m3,
=2×10-4m3,根据阿基米德原理可得:
铝球浸没在水中时受到的浮力F浮=ρ水gV排=ρ水gV铝=1×103kg/m3×10N/kg×2×10-4m3=2N;
(2)设投入铝球后水面上升的高度为△H,则:
△H=
 =
= =
= =0.025m,
=0.025m,水对容器底部增加的压强:
p=ρ水g△H=1×103kg/m3×10N/kg×0.025m=250Pa;
(3)设当铝球露出水面的体积为V露时,绳子会断,此时的浮力为F浮′,
则:F浮′=G-F拉,即ρ水gV排′=G-F拉
V排′=
 =
= =
= =1.4×10-4m3,
=1.4×10-4m3,铝球露出水面的体积:
V露=V-V排′=2×10-4m3-1.4×10-4m3=6×10-5m3.
答:(1)铝球浸没在水中时受到的浮力是2N;
(2)投入铝球后,水对容器底部的压强增加250Pa;
(3)若用一根最多能承受4N拉力的细绳系住铝球缓慢向上拉,当铝球露出水面的体积为1.4×10-4m3时绳子会拉断.
分析:(1)先根据V=
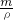 求铝球的体积,铝球浸没在水中时排开水的体积和本身的体积相等,再根据F浮=ρgV排求出铝球浸没在水中受到的浮力;
求铝球的体积,铝球浸没在水中时排开水的体积和本身的体积相等,再根据F浮=ρgV排求出铝球浸没在水中受到的浮力;(2)根据V=Sh求出铝球浸没时容器内水上升的高度,再根据p=ρgh求出容器底部压强的增加量;
(3)根据G=mg可知铝球的重力,绳恰好断掉时绳的拉力为4N,此时水中的铝块受到得浮力等于铝块重减去绳子的拉力,根据阿基米德原理可计算铝块在水中的体积,铝块露出水面的体积V露=V-V排.
点评:本题是一道力学综合题,要求灵活运用密度公式、重力公式、液体压强公式、阿基米德原理和力的合成,难度较大.

练习册系列答案
相关题目
 如图所示,底面积为80cm2的圆筒形容器内装有适量的水,放在水平桌面上.底面积为60cm2、高为12cm的实心圆柱形物体A用细线拴好并悬挂在弹簧测力计下.将圆柱形物体A逐渐浸入圆筒形容器内的水中时(水没有溢出容器),下面的表格中记录了弹簧测力计的示数F与圆柱形物体A下表面离水面的距离h的对应关系.请解答下列问题:(不计细线重,g取10N/kg)
如图所示,底面积为80cm2的圆筒形容器内装有适量的水,放在水平桌面上.底面积为60cm2、高为12cm的实心圆柱形物体A用细线拴好并悬挂在弹簧测力计下.将圆柱形物体A逐渐浸入圆筒形容器内的水中时(水没有溢出容器),下面的表格中记录了弹簧测力计的示数F与圆柱形物体A下表面离水面的距离h的对应关系.请解答下列问题:(不计细线重,g取10N/kg)
| 测量次数 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| h/cm | 0 | 2 | 4 | 6 | 8 | 10 | 12 | 14 | 16 |
| F/N | 9.0 | 7.8 | 6.6 | 5.4 | 4.2 | 3.0 | 1.8 | 1.8 | 1.8 |
(2)在表格中任取一组数据分析说明物体受到的浮力与排开的水所受到的重力的关系,从而证明阿基米德原理的正确性.
(3)物体A在容器内浸没后与未放人物体A前比较,水对容器底产生的压强增加了多少?
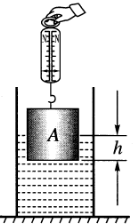 如图所示,底面积为80cm2的圆筒形容器内装有适量的水,放在水平桌面上.底面积为60cm2、高为12cm的实心圆柱形物体A用细线拴好并悬挂在弹簧测力计下.将圆柱形物体A逐渐浸入圆筒形容器内的水中时(水没有溢出容器),下面的表格中记录了弹簧测力计的示数F与圆柱形物体A下表面离水面的距离h的对应关系.请解答下列问题:(不计细线重,g取10N/kg)
如图所示,底面积为80cm2的圆筒形容器内装有适量的水,放在水平桌面上.底面积为60cm2、高为12cm的实心圆柱形物体A用细线拴好并悬挂在弹簧测力计下.将圆柱形物体A逐渐浸入圆筒形容器内的水中时(水没有溢出容器),下面的表格中记录了弹簧测力计的示数F与圆柱形物体A下表面离水面的距离h的对应关系.请解答下列问题:(不计细线重,g取10N/kg) 如图所示,底面积为30cm2平底薄壁塑料杯内装了适量酒精,酒精深度为10cm.(ρ酒精=0.8×103kg/m3)
如图所示,底面积为30cm2平底薄壁塑料杯内装了适量酒精,酒精深度为10cm.(ρ酒精=0.8×103kg/m3) 如图所示,底面积为30cm2平底薄壁塑料杯内装了适量酒精,酒精深度为10cm.(ρ酒精=0.8×103kg/m3)
如图所示,底面积为30cm2平底薄壁塑料杯内装了适量酒精,酒精深度为10cm.(ρ酒精=0.8×103kg/m3)