题目内容
【题目】在探究光的折射规律实验中,某小组将光从空气分别射入水和玻璃中,并记录了如下数据:
空气中的入射角i |
|
|
|
|
水中的折射角r |
|
|
|
|
玻璃中的折射角 |
|
|
|
|
分析表中数据,可以得到一些规律:
(1)当光从一种介质垂直射入到另外一种介质时,光的传播方向______(填“改变”或“不变”)。
(2)光从空气斜射入其他介质时,折射角随着入射角的增大而______(填“增大”或“减小”);分析表中数据猜想,光从空气射入其他介质时,折射角______(填“可能”或“不可能”)达到![]() 。
。
(3)当光线以![]() 入射角从水中射向空气时,折射角等于______
入射角从水中射向空气时,折射角等于______![]() 。
。
(4)根据表中数据分析,用塑料薄膜和水制成一个“水凸透镜”,与外观尺寸相同的玻璃凸透镜相比,“水凸透镜”的焦距更______(填“大”或“小”)。
【答案】不变 增大 不可能 45 大
【解析】
![]() 由表中数据可知,当空气中的入射角i为
由表中数据可知,当空气中的入射角i为![]() 时,水中的折射角r和玻璃中的折射角
时,水中的折射角r和玻璃中的折射角![]() 都为
都为![]() ,故当光从一种介质垂直射入到另一种介质时,传播方向不变;
,故当光从一种介质垂直射入到另一种介质时,传播方向不变;
![]() 由表格中的数据可知:当空气中的入射角i逐渐增大时,折射角也随之增大;但折射角始终小于入射角,故光从空气射入其它介质时,折射角不可能达到
由表格中的数据可知:当空气中的入射角i逐渐增大时,折射角也随之增大;但折射角始终小于入射角,故光从空气射入其它介质时,折射角不可能达到![]() ;
;
![]() 光的折射中,光路是可逆的,由表格数据可知,当光线以
光的折射中,光路是可逆的,由表格数据可知,当光线以![]() 入射角从水中射向空气时,则折射角是
入射角从水中射向空气时,则折射角是![]() ;
;
![]() 由表格可知,入射角相同时,光射入玻璃的折射角为
由表格可知,入射角相同时,光射入玻璃的折射角为![]() ,光射入水中时折射角为
,光射入水中时折射角为![]() ,玻璃对光的偏折能力更强。所以两个外形完全一样的水凸透镜和玻璃凸透镜,玻璃凸透镜的焦距应更短。水凸透镜”的焦距更大。
,玻璃对光的偏折能力更强。所以两个外形完全一样的水凸透镜和玻璃凸透镜,玻璃凸透镜的焦距应更短。水凸透镜”的焦距更大。

【题目】小华在课外探究弹簧的长度与外力的变化关系,利用如图所示实验装置记录了相应实验数据,如下表:
钩码的质量(g) | 0 | 50 | 100 | 150 | 200 | 250 | 300 | 400 |
指针的位置(cm) | 2 | 3 | 4 | 5 | 6 | 7 | 7.5 | 7.5 |
(1)这项研究在实际中的应用是__________;
(2)分析实验数据你可得到的结论是:___________;
(3)小华作出了如下图 所示的三个图像,正确的是_______(填序号)。

A.  B.
B. 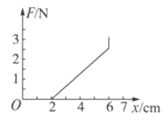 C.
C.