题目内容
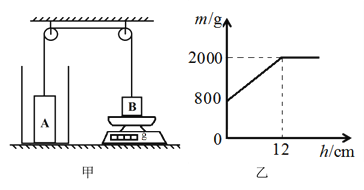
【题目】如图甲所示。一根轻质不可伸长的细线,绕过定滑轮(不计摩擦)将均匀柱体A与B相连,B置于水平放置的电子秤的托盘上,A置于足够高的薄壁柱形容器底部,但与容器底部不挤压。逐渐向容器中加水,得到了电子秤的示数m与容器中水深h之间的关系,如图乙所示。已知B的重力为20N,体积为400cm3,容器重为10N,S容=4SA。求:
(1)柱体B的密度是多少?
(2)柱体 A的重力是多少?
(3)水深为15cm时,柱形容器对水平地面的压强是多少?
【答案】(1)5×103kg/m3;(2)12N;(3)1750Pa
【解析】
(1)知道圆柱体B的重力和体积,根据G=mg求出其质量,根据密度的公式得到B的密度;
(2)A置于足够高的薄壁柱形容器底部时与容器底部不挤压,此时绳子的拉力等于圆柱体A的重力,圆柱体B静止时处于平衡状态时受到竖直向上的支持力、绳子的拉力等于竖直向下的重力,圆柱体B对电子称的压力和电子称对圆柱体B的支持力是一对相互作用力,据此得出它们之间的关系,然后结合h=0时电子秤的示数即可得出A的重力;
(3)由图乙可知,容器内水的深度为12cm以后,电子称的示数不变,且此时电子秤的示数等于圆柱体B的质量,则此时绳子的拉力为零,圆柱体A处于漂浮或悬浮状态;当容器内水的深度恰好为h=12cm时,圆柱体A恰好漂浮,根据阿基米德原理和物体浮沉条件求出容器的底面积;当水深h′=15cm时,圆柱体A处于漂浮或悬浮状态,排开水的重力和自身的重力相等,据此求出容器内水和圆柱体A的重力之和,根据水平面上物体的压力和自身的重力相等结合压强的公式求出柱形容器对水平地面的压强。
(1)由G=mg可得,圆柱体B的质量:![]() ,
,
则柱体B的密度:![]() ;
;
(2)因A置于足够高的薄壁柱形容器底部时与容器底部不挤压,所以此时绳子的拉力等于圆柱体A的重力F1=GA--------①
圆柱体B静止时处于平衡状态,受到竖直向上的支持力、绳子的拉力以及竖直向下的重力作用,所以,由平衡条件可得:F支持+F1=GB------------------②
又因圆柱体B对电子称的压力和电子称对圆柱体B的支持力是一对相互作用力,
所以,F压=F支持----------------③
因电子称的示数等于圆柱体B对电子称的压力,所以,由图乙可知,h=0时,电子秤的示数m1=800g=0.8kg,则F压=m1g-------------------④
由①②③④可得:GA=GB-m1g=20N-0.8kg×10N/kg=12N;
(3)由图乙可知,容器内水的深度为12cm以后,电子称的示数不变,且恒为m′=2000g=2kg,因此时电子秤的示数等于圆柱体B的质量,所以,此时绳子的拉力为零,圆柱体A处于漂浮或悬浮状态,当容器内水的深度恰好为h=12cm时,圆柱体A排开水的体积V排A=SAh,因物体漂浮或悬浮时受到的浮力等于自身的重力,由阿基米德原理可得:GA=F浮A=ρ水gV排A=ρ水gSAh,则A的底面积:![]() ,
,
容器的底面积:S容=4SA=4×0.01m2=0.04m2,当水深h′=15cm时,圆柱体A仍然处于漂浮或悬浮状态,排开水的重力和自身的重力相等,所以,容器内水和圆柱体A的重力之和:G水和A=m水和Ag=ρ水S容h′g=1.0×103kg/m3×0.04m2×0.15m×10N/kg=60N,柱形容器对水平地面的压力:F=G水和A+G容=60N+10N=70N,柱形容器对水平地面的压强:![]() 。
。

 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案