题目内容
测定组成实心金属球金属的密度.(1)其中一组同学用如图1所示的方法,杠杆的重力忽略不计,请你将下列实验步骤补充完整.
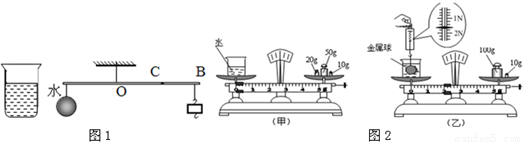
①将金属球挂在杠杆的A段,将钩码悬挂在B点,杠杆在水平位置平衡.
②将金属球没入水中,此时将钩码移动到C点,杠杆仍在水平位置平衡.
③用刻度尺测量AO的长度为L1;
④______;
⑤金属密度的表达式为______;
(2)另一组的同学用如图所示的方法测定实心金属球金属的密度.请你根据图2填写下表,跟同学们一起完成实验.(g=10N/kg)
| 甲图中砝码和游码总质量值m1/g | 乙图中砝码和游码总质量值m2/g | 乙图中弹簧测力计示数F/N | 金属球的体积V/cm3 | 金属球的质量m/g | 金属球的密度ρ/g/cm3 |
| 80 | ______ | ______ | ______ | ______ | ______ |
【答案】分析:(1)④为了能够利用杠杆的平衡条件进行分析,必须要测量出杠杆其他部分的长度;⑤根据杠杆的平衡条件,列出两次时的平衡方程,组成方程组进行求解,即可求得金属球的密度.
(2)此题前两空比较简单,关键在于体积计算:弹簧测力计的示数F不是金属球的重力G,也不是球受到的浮力F浮.而是G-F浮,F浮应该是左盘受到的压力的增加量,即右盘砝码增加量对应的重力,因为金属球浸没在水中受到竖直向上的浮力,金属球给水一个竖直向下的反作用力.根据浮力的大小计算出物体的体积,由浮力和测力计的示数计算出物体的重力,从而得出其质量,进而求金属球的密度.
解答:解:
(1)④用刻度尺测出OB的长度为L2,OC的长度为L3;
⑤杠杆第一次平衡时:m金L1=m码L2,
杠杆第二次平衡时:(m金g-ρ水 g)L1=m码gL3,
g)L1=m码gL3,
解方程组得:ρ金= ρ水;
ρ水;
(2)乙图中砝码和游码总质量值为:m2=100g+10g+2g=112g;
测力计的分度值为0.2N,所以乙图中弹簧测力计的示数为:F=1.6N;
甲图中天平的读数是:m1=80g,所以增加的重力为:△G=(m2-m1)g=(112-80)×10-3kg×10N/kg=0.32N;
所以浮力的大小为0.32N.
根据公式F浮=ρ水gV排得:
V排= =
= =0.32×10-4m3=32cm3
=0.32×10-4m3=32cm3
因为F=G-F浮,所以G=F+F浮=1.6N+0.32N=1.92N
金属球的质量为:m= =
=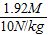 =0.192kg=192g;
=0.192kg=192g;
金属球的密度为:ρ= =
= =6g/cm3
=6g/cm3
故答案为:(1)④用刻度尺测出OB的长度为L2;OC的长度为L3;⑤ ρ水;
ρ水;
(2)112,1.6,32,192,6.
点评:第一问:利用杠杆的平衡条件列方程,是解决此题的关键方法;
第二问:密度测量几乎是每年中考的必考题目,本题有别于其他密度测量的考法,别具一格,尤其是矿石的体积具有极强的迷惑性,属于难题.
(2)此题前两空比较简单,关键在于体积计算:弹簧测力计的示数F不是金属球的重力G,也不是球受到的浮力F浮.而是G-F浮,F浮应该是左盘受到的压力的增加量,即右盘砝码增加量对应的重力,因为金属球浸没在水中受到竖直向上的浮力,金属球给水一个竖直向下的反作用力.根据浮力的大小计算出物体的体积,由浮力和测力计的示数计算出物体的重力,从而得出其质量,进而求金属球的密度.
解答:解:
(1)④用刻度尺测出OB的长度为L2,OC的长度为L3;
⑤杠杆第一次平衡时:m金L1=m码L2,
杠杆第二次平衡时:(m金g-ρ水
 g)L1=m码gL3,
g)L1=m码gL3,解方程组得:ρ金=
 ρ水;
ρ水;(2)乙图中砝码和游码总质量值为:m2=100g+10g+2g=112g;
测力计的分度值为0.2N,所以乙图中弹簧测力计的示数为:F=1.6N;
甲图中天平的读数是:m1=80g,所以增加的重力为:△G=(m2-m1)g=(112-80)×10-3kg×10N/kg=0.32N;
所以浮力的大小为0.32N.
根据公式F浮=ρ水gV排得:
V排=
 =
= =0.32×10-4m3=32cm3
=0.32×10-4m3=32cm3因为F=G-F浮,所以G=F+F浮=1.6N+0.32N=1.92N
金属球的质量为:m=
 =
=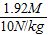 =0.192kg=192g;
=0.192kg=192g; 金属球的密度为:ρ=
 =
= =6g/cm3
=6g/cm3故答案为:(1)④用刻度尺测出OB的长度为L2;OC的长度为L3;⑤
 ρ水;
ρ水;(2)112,1.6,32,192,6.
点评:第一问:利用杠杆的平衡条件列方程,是解决此题的关键方法;
第二问:密度测量几乎是每年中考的必考题目,本题有别于其他密度测量的考法,别具一格,尤其是矿石的体积具有极强的迷惑性,属于难题.

练习册系列答案
相关题目
 (2010?西城区二模)测定组成实心金属球金属的密度.如图所示,杠杆的重力忽略不计,请你将下列实验步骤补充完整.
(2010?西城区二模)测定组成实心金属球金属的密度.如图所示,杠杆的重力忽略不计,请你将下列实验步骤补充完整.