题目内容
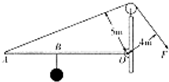 如图所示,OA是起重机的吊臂,可绕O点转动.在距O点6m远的B处吊有重3000N的物体.为保证吊臂在水平位置平衡,用绳子绕过定滑轮拉住吊臂.则图中绳子对杠杆0A拉力的力臂为
如图所示,OA是起重机的吊臂,可绕O点转动.在距O点6m远的B处吊有重3000N的物体.为保证吊臂在水平位置平衡,用绳子绕过定滑轮拉住吊臂.则图中绳子对杠杆0A拉力的力臂为5
5
m,拉力F为3600
3600
N.将吊臂缓慢拉起,使A点升高2m的过程中,拉力变小
小
.(绳重、吊臂重、摩擦均不计)分析:(1)支点到力的作用线的垂直距离是力的力臂,根据图示确定拉力的力臂;由杠杆平衡条件求出拉力的大小;
(2)根据图示判断将吊臂缓慢拉起,使A点升高2m的过程中,力臂如何变化,然后由杠杆平衡条件判断拉力如何变化.
(2)根据图示判断将吊臂缓慢拉起,使A点升高2m的过程中,力臂如何变化,然后由杠杆平衡条件判断拉力如何变化.
解答:解:(1)杠杆阻力为物重G=3000N,阻力臂为OB=6m,
由图可知绳子绕过定滑轮只改变了力的方向,
因此动力臂为5m.根据杠杆平衡条件:
F1l1=F2l2即F×5m=3000N×6m,所以F=3600N.
(2)吊臂OA在水平位置时,阻力(物体重力)竖直向下,
与杠杆OA垂直,OB是力臂,此时力臂最大,是OB间的长度为6m;
将吊臂缓慢拉起,使A点升高的过程中,阻力与杠杆OA不再垂直,
杠杆与水平方向间的夹角变小θ,因此阻力臂L阻=OAsinθ变小,
动力臂L阻=OAcosθ变大,阻力不变,由杠杆平衡条件:
动力×动力臂=阻力×阻力臂可知:拉力变小.
故答案为:5;3600;小.
由图可知绳子绕过定滑轮只改变了力的方向,
因此动力臂为5m.根据杠杆平衡条件:
F1l1=F2l2即F×5m=3000N×6m,所以F=3600N.
(2)吊臂OA在水平位置时,阻力(物体重力)竖直向下,
与杠杆OA垂直,OB是力臂,此时力臂最大,是OB间的长度为6m;
将吊臂缓慢拉起,使A点升高的过程中,阻力与杠杆OA不再垂直,
杠杆与水平方向间的夹角变小θ,因此阻力臂L阻=OAsinθ变小,
动力臂L阻=OAcosθ变大,阻力不变,由杠杆平衡条件:
动力×动力臂=阻力×阻力臂可知:拉力变小.
故答案为:5;3600;小.
点评:对于杠杆类习题首先从确定动力、阻力、动力臂、阻力臂入手.动态杠杆问题要分析好变量与不变量.再根据杠杆平衡条件解答.

练习册系列答案
相关题目
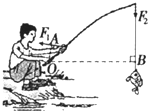 小华用钓鱼竿钓起重为15N的鱼,如图所示,OA=0.4m,OB=2m.下列说法正确的是( )
小华用钓鱼竿钓起重为15N的鱼,如图所示,OA=0.4m,OB=2m.下列说法正确的是( )| A、用钓鱼竿钓鱼费距离 | B、钓鱼竿是个省力杠杆 | C、手对鱼杆的拉力F1的大小为75N | D、手对鱼杆的拉力F1的大小为3N |
小华用钓鱼杆钓起重为15N的鱼,如图所示,OA=0.4m,OB=2m。下列说法中正确的是 
| A.用的鱼杆费距离 |
| B.用的鱼杆是省力杠杆 |
| C.手对鱼杆拉力大小等于75N |
| D.手对鱼杆拉力大小等于3N |


