Question

【题目】如图是利用电子秤监控水库水位的模拟装置，由长方体A和B、滑轮组、轻质杠杠CD、电子秤等组成．杠杠始终在水平位置平衡．已知OC：OD=1：2，A的体积为0.02m3 ， A重为400N，B重为150N，动滑轮重100N，不计绳重与摩擦（ρ水=1.0×103kg/m3）．求：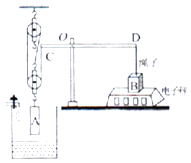
（1）A的密度；
（2）单独使用该滑轮组在空气中匀速提升A时的机械效率；
（3）水位上涨到A的上表面时，A受到的浮力；
（4）水位上涨过程中，电子秤所受的最大压力．

Answer 1

【答案】
（1）解：长方体A的质量，根据G=mg可得：

m= = =40kg，

长方体A的密度ρ= = =2×103kg/m3，

答：A的密度为2×103kg/m3；

（2）解：单独使用该滑轮组在空气中匀速提升A时，n=3，根据η=W有/W总×100%可得：

机械效率η= ×100%= ×100%= ×100%= ×100%=80%；

答：单独使用该滑轮组在空气中匀速提升A时的，机械效率为80%；

（3）解：当水位上涨到A的上表面时，因为A浸没水中，所以V排=VA，

根据F=ρgV排可得：

A受到的浮力：F浮=ρgV排=1.0×103kg/m3×10N/kg×0.02m3=200N；

答：当水位上涨到A的上表面时，A物体浸没在水后所受浮力的大小为200N；

（4）解：水位上涨过程中，因要求电子秤所受的最大压力，即A浸没水中，受到的浮力最大F浮=200N，

n=3，根据力的平衡有：FC= ，

FC= =100N，

根据相互作用力大小相等可知，A对C端拉力与C对A物体拉力大小相等，所以作用在杠杆C端的力，因杠杆始终在水平位置平衡，O为支点，

根据F1L1=F2L2可得：

FC L1=FDL2

100N×OC=OD×FD

解得：FD= = =50N

对B物体受力平衡，所以电子秤受到B物体对它的最大压力：

F压=FN=GB﹣FD=150N﹣50N=100N．

答：水库中的水刚好浸没物体A时，B物体对电子秤最大的压力是100N．

【解析】（1）根据m= 计算长方体的质量，再根据ρ= 计算长方体的密度；（2）单独使用该滑轮组在空气中匀速提升A时，n=3，根据η= = 可求得机械效率；（3）已知物块A的体积（物块A的顶部刚没入水面时排开水的体积），利用阿基米德原理求物块A所受的浮力；（4）对滑轮组进行受力分析，求出作用在C端的力，再利用杠杆平衡的条件求出D端的作用力，电子秤受到B的压力等于重力和拉力的合力．
【考点精析】解答此题的关键在于理解密度的计算的相关知识，掌握密度公式：ρ = m/v，以及对杠杆的平衡条件的理解，了解杠杆平衡：杠杆在动力和阻力的作用下静止或匀速转动时，称为杠杆平衡．杠杆平衡是力和力臂乘积的平衡，而不是力的平衡．杠杆平衡的条件：动力 ×动力臂 = 阻力 ×阻力臂即：F1 L1 = F2 L2可变形为 ：F1 / F2 = L1 / L2．