题目内容
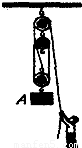
 某工地上用如图所示的滑轮组,匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)
某工地上用如图所示的滑轮组,匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求:(1)滑轮组做的有用功;
(2)物体上升的速度;
(3)拉力F的大小;
(4)若用该滑轮组吊起6250N的重物时机械效率为多少?
分析:(1)知道物体的质量,可利用公式G=mg计算出物体的重力,又知道物体上升的高度,可利用公式W有用=Gh计算出克服重力所做的有用功.
(2)从图可知,该滑轮组有3段绳子吊着物体,从而可以计算出拉力移动的距离,知道滑轮组的机械效率,可利用公式W总=
计算出所做的总功,再由功率的公式P=
计算出做功时间t,又知道物体上升的高度,利用速度公式求物体上升的速度.
(3)首先利用公式F=
计算出拉力的大小;
(4)不计绳重和摩擦,知道物体的重力和拉力的大小,可利用公式F=
(G+G动)计算出动滑轮的重力,动滑轮的重力不变,若该滑轮组吊起6250N的重物,再利用F=
(G+G动)计算出拉力的大小.再利用公式η=
=
=
=
计算出此时滑轮组的机械效率.
(2)从图可知,该滑轮组有3段绳子吊着物体,从而可以计算出拉力移动的距离,知道滑轮组的机械效率,可利用公式W总=
| W有用 |
| η |
| W |
| t |
(3)首先利用公式F=
| W |
| s |
(4)不计绳重和摩擦,知道物体的重力和拉力的大小,可利用公式F=
| 1 |
| 3 |
| 1 |
| 3 |
| W有用 |
| W总 |
| Gh |
| Fs |
| Gh |
| Fnh |
| G |
| nF |
解答:解:
(1)∵m=500kg,g=10N/kg,
∴物体的重力为:G=mg=500kg×10N/kg=5000N;
而h=0.8m,
∴滑轮组做的有用功为:W有=Gh=5000N×0.8m=4000J.
(2)从图可知,该滑轮组有3段绳子吊着物体,
∴拉力移动的距离为:s=3h=3×0.8m=2.4m;
而此滑轮组的机械效率为η=80%,
∴所做的总功为:W总=
=
=5000J;
又∵拉力F的功率为P=2500W,
∴做功的时间为:t=
=
=2s,
则物体上升的速度为:v=
=
=0.4m/s.
(3)∵W总=Fs,
∴拉力的大小为:F=
=
=
N.
(4)∵不计绳重和摩擦,F=
(G+G动),
∴G动=3F-G=3×
-5000N=1250N.
用该滑轮组吊起6250N的重物时,拉力的大小为:F′=
(G′+G动)=
(6250N+1250N)=2500N;
∴滑轮组的机械效率为:η′=
=
≈83.3%.
答:(1)滑轮组做的有用功为4000J.
(2)物体上升的速度为0.4m/s.
(3)动滑轮的重力为1250N.
(4)若用该滑轮组吊起6250N的重物则拉力为2500N,此时的机械效率为83.3%.
(1)∵m=500kg,g=10N/kg,
∴物体的重力为:G=mg=500kg×10N/kg=5000N;
而h=0.8m,
∴滑轮组做的有用功为:W有=Gh=5000N×0.8m=4000J.
(2)从图可知,该滑轮组有3段绳子吊着物体,
∴拉力移动的距离为:s=3h=3×0.8m=2.4m;
而此滑轮组的机械效率为η=80%,
∴所做的总功为:W总=
| W有用 |
| η |
| 4000J |
| 80% |
又∵拉力F的功率为P=2500W,
∴做功的时间为:t=
| W总 |
| P |
| 5000J |
| 2500W |
则物体上升的速度为:v=
| h |
| t |
| 0.8m |
| 2s |
(3)∵W总=Fs,
∴拉力的大小为:F=
| W总 |
| s |
| 5000J |
| 2.4m |
| 6250 |
| 3 |
(4)∵不计绳重和摩擦,F=
| 1 |
| 3 |
∴G动=3F-G=3×
| 6250 |
| 3 |
用该滑轮组吊起6250N的重物时,拉力的大小为:F′=
| 1 |
| 3 |
| 1 |
| 3 |
∴滑轮组的机械效率为:η′=
| G′ |
| nF′ |
| 6250N |
| 3×2500N |
答:(1)滑轮组做的有用功为4000J.
(2)物体上升的速度为0.4m/s.
(3)动滑轮的重力为1250N.
(4)若用该滑轮组吊起6250N的重物则拉力为2500N,此时的机械效率为83.3%.
点评:本题中用到的都是基本公式,但数据间的关系却较为复杂,考查的角度与不尽相同,因此,最大的难点是如何灵活运用公式,搞清正确的数据关系,最终才能顺利求解.本题关键有二:一是n的确定(直接从动滑轮上引出的绳子股数);二是利用好不计绳重和摩擦时,拉力和物重的关系:F=
(G轮+G物).
| 1 |
| n |

练习册系列答案
相关题目
 某工地上用如图所示的滑轮组匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率为2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求:
某工地上用如图所示的滑轮组匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率为2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求: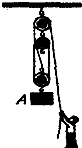 某工地上用如图所示的滑轮组,匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率为2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求:
某工地上用如图所示的滑轮组,匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率为2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求: 某工地上用如图所示的滑轮组匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率为2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求:
某工地上用如图所示的滑轮组匀速提升质量为500kg的物体,在物体上升0.8m的过程中,拉力F的功率为2500W,此滑轮组的机械效率为80%,不计绳重和摩擦.(g=10N/kg)求: