题目内容
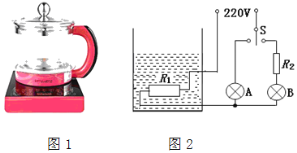
【题目】如图,电源电电压不变,定值电阻R1=6Ω,电流表的量程为0~0.6A,电压表的量程为0~3V,滑动变阻器R2的规格为“40Ω 1A”,闭合开关后,当滑片P置于M点时,电流表示数为0.3A,当滑片P置于N点时,电流表示数变化了0.1A,且滑动变阻器连入电路中的阻值![]() 。
。

(1)求定值电阻R1前后两次电功率之比;
(2)求电源电压;
(3)在不损坏元件的情况下,求出滑动变阻器的取值范围。
【答案】(1)定值电阻R1前后两次电功率之比为9:4;(2)电源电压为3.6V;(3)在不损坏元件的情况下,滑动变阻器的取值范围为0Ω~30Ω。
【解析】
(1)滑片由M点滑到N点,电阻变大,电路中的电流减小,求出滑片P置于N点时电路中的电流,再根据P=I2R求出定值电阻R1前后两次电功率;
(2)根据电源电压不变列出等式,求出电源电压;
(3)根据电流表量程和滑动变阻器规格分析电路中的最大电流,进而求出滑动变阻器的最小阻值;
电压表测量滑动变阻器两端的电压,其示数最大时,滑动变阻器连入电路中的阻值最大,根据分压特点求出连入电路的最大阻值。
(1)滑片由M点滑到N点,电阻变大,电路中的电流减小,所以滑片P置于N点时电路中的电流:
IN=IM﹣0.1A=0.3A﹣0.1A=0.2A,
定值电阻R1前后两次电功率之比:
![]()
(2)滑片P置于M点时,电源电压U=IM(R1+RM),
滑片P置于N点时,电源电压U=IN(R1+RN),
RN=2RM,
所以0.3A×(R1+RM)=0.2A×(R1+2RM),
解得RM=R1=6Ω,
电源电压:
U=IM(R1+RM)=0.3A×(6Ω+6Ω)=3.6V;
(3)根据电流表量程和滑动变阻器规格可知,电路中的最大电流为I大=0.6A,
由欧姆定律可得,电路总电阻:
![]()
滑动变阻器连入电路的最小阻值:
R滑小=R﹣R1=6Ω﹣6Ω=0Ω;
电压表的量程为0~3V,滑动变阻器两端的最大电压U滑=3V,
R1两端的电压U1=U﹣U滑=3.6V﹣3V=0.6V,
根据串联电路的分压特点可知:![]()
解得R滑大=30Ω,
所以在不损坏元件的情况下,滑动变阻器的取值范围为0Ω~30Ω。

 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案