题目内容
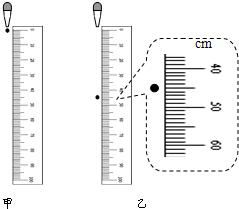
 小强猜想:水滴开始下落的过程可能是变速直线运动.为此,他做了这样的实验:将米尺竖直放置在地板上,滴管嘴与米尺的0刻度线平齐,如图所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中.
小强猜想:水滴开始下落的过程可能是变速直线运动.为此,他做了这样的实验:将米尺竖直放置在地板上,滴管嘴与米尺的0刻度线平齐,如图所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中.| 画面 | 水滴已运动的时间t(s) | 水滴落下的距离h(cm) |
| 第8帧 | 0 | 0 |
| 第10帧 | 0.1 | 5.0 |
| 第12帧 | 0.2 | 20.0 |
| 第14帧 | A | B |
| 第16帧 | 0.4 | C |
0.3
0.3
、45.0
45.0
、80.0
80.0
.(2)根据表中的数据,可以计算出该墨水从第14帧到第16帧的平均速度是
3.5
3.5
m/s.(3)小强分析表中的数据发现,水滴下落的距离与
时间的平方
时间的平方
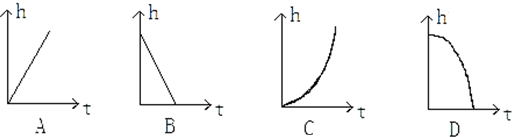
成正比.(4)水滴下落时,水滴与地板间的距离h′与水滴运动的时间t的函数图象可能是图中的
D
D
.
(5)若拍摄第10、12、14、16帧照片时水滴下落的速度分别为1m/s、2m/s、3m/s、4m/s,则重力对水滴做功的功率P随时间t变化的图象可能是图中的
A
A

分析:(1)由图可知,第14帧画面显示墨水滴在0.3s时的位置;分析前四组数据可知,墨水滴下落的距离和相应时间的平方成正比,根据以上分析完成表格;
(2)根据表格中的数据得出从第14帧到第16帧高度的变化率和时间,利用速度公式求出平均速度;
(3)分析表中的数据发现墨水滴下落的距离和相应时间的平方成正比;
(4)根据墨水滴下落的距离和相应时间的平方成正比可知,水滴与地板间的距离和水滴已运动的时间不成正比例减小,据此判断图象.
(5)根据P=Gv可知,速度倍增,则功率也应该倍增,据此判断图象.
(2)根据表格中的数据得出从第14帧到第16帧高度的变化率和时间,利用速度公式求出平均速度;
(3)分析表中的数据发现墨水滴下落的距离和相应时间的平方成正比;
(4)根据墨水滴下落的距离和相应时间的平方成正比可知,水滴与地板间的距离和水滴已运动的时间不成正比例减小,据此判断图象.
(5)根据P=Gv可知,速度倍增,则功率也应该倍增,据此判断图象.
解答:解:
(1)由图可知,墨水滴在0.3s时,下落的距离为45cm,故A为0.3,B为45.0;
分析前四组数据可知,水滴落下的距离h和水滴已运动时间t的平方的比值
=
=
=500cm/s2,
即墨水滴下落的距离和相应时间的平方成正比,
所以hc=500cm/s2×(0.4s)2=80cm;
(2)由表格中的数据可知,该墨水从第14帧到第16帧:
△h=80.0cm-45cm=35cm=0.35m,
t=0.4s-0.3s=0.1s,
平均速度v=
=
=3.5m/s;
(3)由水滴落下的距离h和水滴已运动时间t的平方的比值不变可知,水滴下落的距离与时间的平方成正比;
(4)∵水滴下落的距离与时间的平方成正比,
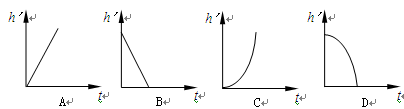
∴水滴与地板间的距离h′与水滴已运动的时间t的函数图象不成正比,且水滴与地板间的距离h′随时间t变长而减小,故D符合.
(5)根据P=Gv可知,速度倍增,则功率也应该倍增,功率随时间倍增的只有A图象符合,故选A.
故答案为:
(1)0.3;45.0;80.0;
(2)3.5;
(3)时间的平方;
(4)D;
(5)A.
(1)由图可知,墨水滴在0.3s时,下落的距离为45cm,故A为0.3,B为45.0;
分析前四组数据可知,水滴落下的距离h和水滴已运动时间t的平方的比值
| 5.0cm |
| (0.1s)2 |
| 20.0cm |
| (0.2s)2 |
| 45.0cm |
| (0.3s)2 |
即墨水滴下落的距离和相应时间的平方成正比,
所以hc=500cm/s2×(0.4s)2=80cm;
(2)由表格中的数据可知,该墨水从第14帧到第16帧:
△h=80.0cm-45cm=35cm=0.35m,
t=0.4s-0.3s=0.1s,
平均速度v=
| △h |
| t |
| 0.35m |
| 0.1s |
(3)由水滴落下的距离h和水滴已运动时间t的平方的比值不变可知,水滴下落的距离与时间的平方成正比;
(4)∵水滴下落的距离与时间的平方成正比,
∴水滴与地板间的距离h′与水滴已运动的时间t的函数图象不成正比,且水滴与地板间的距离h′随时间t变长而减小,故D符合.
(5)根据P=Gv可知,速度倍增,则功率也应该倍增,功率随时间倍增的只有A图象符合,故选A.
故答案为:
(1)0.3;45.0;80.0;
(2)3.5;
(3)时间的平方;
(4)D;
(5)A.
点评:本题考查了刻度尺的读数、平均速度的计算等,关键是会分析表格中的数据得出“水滴下落的距离与时间的平方成正比”.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 小强猜想:水滴开始下落的过程可能是变速直线运动.为此,他做了这样的实验:将米尺竖直放置,滴管嘴与米尺的0刻度线平齐,如图甲所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中.
小强猜想:水滴开始下落的过程可能是变速直线运动.为此,他做了这样的实验:将米尺竖直放置,滴管嘴与米尺的0刻度线平齐,如图甲所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中.(1)图乙是小强选出的第14帧画面,请你根据该帧画面提供的信息完成下表的填写.
(2)根据表中的数据,可以证明小强的猜想是
(3)小强分析表中的数据,无法确定水滴下落的距离与运动时间之间的定量关系,进而猜想:水滴下落的距离与运动时间的平方之间可能存在定量关系.请你在答题卡的如图丙中,根据下表中的数据作出水滴下落的距离h与水滴运动时间的平方t2之间的关系图,由图象得到h与t2的关系是
| 画面 | 水滴已运动的时间t(s) | 水滴下落的距离h(cm) |
| 第8帧 | 0 | 0 |
| 第10帧 | 0.1 | 5.0 |
| 第12帧 | 0.2 | 20.0 |
| 第14帧 | ||
| 第16帧 | 0.4 | 79.8 |
(14分)小强猜想:水滴开始下落的过程可能是变速直线运动。为此,他做了这样的实验:将米尺竖直放置在地板上,滴管嘴与米尺的0刻度线平齐,如图11所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中。
| 画面 | 水滴已运动的时间t(s) | 水滴落下的距离h(cm) |
| 第8帧 | 0 | 0 |
| 第10帧 | 0.1 | 5.0 |
| 第12帧 | 0.2 | 20.0 |
| 第14帧 | A | B |
| 第16帧 | 0.4 | C |

(1)上图是小强选出的第14帧画面的放大图,请你根据该帧画面提供的信息思考表中的A、B、C三处分别应填写的数据是________、________、________。
(2)根据表中的数据,可以计算出该墨水从第14帧到第16帧的平均速度是 m/s。
(3)小强分析表中的数据发现,水滴下落的距离与____________成正比。
(4)水滴下落时,水滴与地板间的距离h’与水滴运动的时间t的函数图象可能是下图中的( )
(5)若拍摄第10、12、14、16帧照片时水滴下落的速度分别为1m/s、2 m/s、3 m/s、4 m/s,则重力对水滴做功的功率P随时间t变化的图象可能是下图中的( )
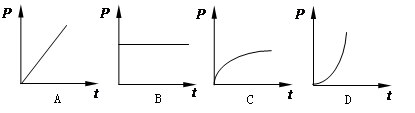
小强猜想:水滴开始下落的过程可能是变速直线运动。为此,他做了这样的实验:将米尺竖直放置,滴管嘴与米尺的0刻度线平齐,如图所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档[该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面]摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中。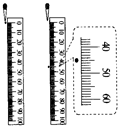
| 画面 | 水滴已运动的时间t(s) | 水滴下落的距离h(cm) |
| 第8帧 | 0 | 0 |
| 第10帧 | 0.1 | 5.0 |
| 第12帧 | 0.2 | 20.0 |
| 第14帧 | | |
| 第16帧 | 0.4 | 79.8 |
(2)根据表中的数据,可以证明小强的猜想是 (选填“正确”或“错误”)。该墨水下落0.2s的平均速度是 m/s。
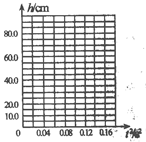
(3)小强分析表中的数据,无法确定水滴下落的距离与运动时间之间的定量关系,进而猜想:水滴下落的距离与运动时间的平方之间可能存在定量关系。请你在下面的图中,根据表中的数据作出水滴下落的距离h与水滴运动时间的平方t2之间的关系图,由图象得到h与t2的关系是 (选填“成正比”、“成反比”或“不确定”)。
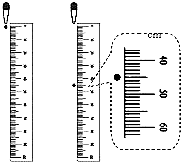 小强猜想:水滴开始下落的过程可能是变速直线运动.为此,他做了这样的实验:将米尺竖直放置,滴管嘴与米尺的0刻度线平齐,如图8所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中.
小强猜想:水滴开始下落的过程可能是变速直线运动.为此,他做了这样的实验:将米尺竖直放置,滴管嘴与米尺的0刻度线平齐,如图8所示,当墨水刚从滴管嘴滴出时,用数码照相机的摄影档(该相机摄出视频影像,每隔0.05s摄下一帧(即一幅)静态画面),摄下该滴墨水自由下落的全过程;接着在媒体播放器上逐帧观看拍下的静态画面,发现第8帧画面上墨水才从滴管滴出,他从第8帧画面开始,每隔2帧选出一张画面,读出有关信息并填入下表中.